Review of "Chemical and forensic analysis of JFK assassination bullet lots: Is a second shooter possible?"

Kenneth A. Rahn
3 June 2007 (Slightly updated 18 June 2007)

Background
    There is a contingent of JFK researchers who refuse to accept the importance of Dr. Vincent P. Guinn's analyses of the bullet fragments by neutron activation (NAA). The reason, of course, is that these analyses provide the strongest evidence for only two bullets having hit the men. This gives the lie to all sorts of conspiracy theories, and so cannot be tolerated by most JFK conspiracy believers.
    When Larry Sturdivan and I published our two articles on the NAA and its implications for the assassination in 2004, the drumbeat of criticism intensified. It reached a first peak in July of 2006, when Randich and Grant published a rebuttal in Journal of Forensic Sciences. That article dealt with metallurgy and statistics, and was hailed as the end of the NAA. Unfortunately for the revisionists, the article was deeply flawed, and did not come close to proving any of its contentions. I wrote an extensive rebuttal on its metallurgical aspects and posted it (click here), but it was largely ignored by the believers.
    Now comes a second article and a second peak of publicity. The article is entitled Chemical and forensic analysis of JFK assassination bullet lots: Is a second shooter possible?, and was written by Cliff Spiegelman, William A. Tobin, William D. James, Simon J. Sheather, Stuart Wexler, and D. Max Roundhill. It will be published by Annals of Applied Statistics. It is better than the first, mostly because it presents new measurements on WCC/MC bullets. But it is also deeply flawed, and does not prove its contentions, even though it is currently being given a great deal of press. Its own data show that the new bullets did not represent the full population of bullets, and so cannot be generalized from.
    Thus the NAA revisionists are now 0 for 2.

General comments
    Status of article. Most of the publicity to date has not stressed that the actual article has not yet appeared. This is important because the final article will include on-line supporting material, presumably providing details of the analyses and the calculations of probability. Thus it is impossible at present to fully critique the article. Thus this review should be considered provisional.
    Technical quality. The article is written quite poorly. It would not be acceptable in my scientific writing course. Small errors include misspelling Mr. Wexler's town and high school ("Highstown" instead of "Hightstown"), misspelling Connally's name (Connelly), confusing "later" and "latter," using "lead" instead of "led," giving a wrong caption for their Table 1 ("How bullets are matched and our bullet number one from lot 6003," which has nothing to do with Table 1), and giving a nonsensical caption for Table 2 ("Bullet # 1 lot 6003 measurements by radial location and combined giving summary statistics for antimony and silver"). The abstract refers to a match to an assassination fragment with one of ten test bullets, whereas the text notes correctly that there were 30 test bullets. All these things mean that the writers were hurried or careless, and that no one proofread the final product, i.e., that it was rushed to print.
    Larger errors are present, too. The sections are nonstandard, which makes it difficult to look for materials. Paragraphs jump between topics with no warning. The authors' bullets and analytical procedure are first discussed under "The brand of bullets believed to be used in the Kennedy assassination," where no one would think to look. The number of bullets proposed by Guinn is also discussed here, as are the two Rahn/Sturdivan papers, sample sizes, and heterogeneity. The section "Statistical analysis of Dr. Guinn's data" is mostly devoted to the authors' work instead. Only one of the two terms in Bayes (sic) theorem is discussed, yet a conclusion is derived from the product of the terms. Meaningless sentences appeared, such as "The new analyses show that bullet fragments involved in the assassination are not nearly as rare as previously reported."
    Motivation. The stated motivation was to show that Guinn's conclusion about only two bullets accounting for the five fragments is open to serious question. That would in theory open the door to one or more additional shooters. But if so, why did the authors go to such trouble? After all, there is zero physical evidence for a second shooter. Something else must have been driving this work forward.
    The strange question of matches within a box. Accidental matches between WCC/MC bullets are the core of this article (because they might show the presence or one or more additional bullets and shooters). The Rahn/Sturdivan articles had based their calculations for an accidental match on MC bullets from all four lots, because there would be no way of knowing from which lots any given bullets originated. (In fact, we even have no idea which lots Oswald's WCC/MC bullets came from.) But Spiegelman et al. feel differently. They state, without further comment, "We think a more relevant population for consideration is that consisting of bullets within the same box of Western Cartridge Company Mannlicher-Carcano bullets." This amounts to requiring that the two shooters would draw their bullets from the same box, which seems unrealistically restrictive. Who is to say that there weren't at least two boxes of bullets involved? Their approach seems to be designed to raise the probability of accidental matches (and additional shooters).

Samples and analysis
    The bullets. The bullets discussed in this article were drawn from three boxes of MC bullets. The authors state that it is not clear which of the four lots they represent. They say that one box is definitely from lot 6000, and one definitely from lot 6003. The third box, however, may be from lot 6003. They call it 6003P, where P stands for "putative." So if we accept their judgment, they have studied only two of the four lots. If we disagree with their judgment, it could be three of the lots. (Independent information provided recently to me confirms that 6003P was really from lot 6003.)
    Does this matter? Probably not very much. Larry Sturdivan and I found that although the lots differed in average concentration of antimony (Sb), the spread within each lot was large enough to make them more similar than different. The overlap created a surprisingly uniform distribution of Sb for the merged sets.
    These bullets have already been analyzed for trace elements by Tom Pinkston. He used inductively coupled plasma analysis (ICP), which is a "wet" technique. That means that the samples have to be dissolved first. By contrast, samples for NAA are not dissolved, but analyzed dry (in little pieces). The NAA procedure is more reliable because one can never be sure that the dissolution process dissolves everything, or that all the dissolved material is carried through the various steps in the analysis. So Spiegelman et al. rightly felt that they had to return to NAA to properly debunk Guinn/Rahn/Sturdivan.
    Getting samples from the bullets. The authors analyzed ten bullets from each of the three boxes. It is hard to find from the article how they extracted samples of lead from the bullets. Their basic approach was to take three samples from each bullet. (Guinn took four.) From where in the bullet? They just say "Efforts were made to maximize the spread of locations sampled within a bullet." The basic results for each bullet were presumably the means and standard deviations of these three measurements (although this was not stated explicitly). For the ten bullets in lot 6003, however, three samples were taken from each of the three locations, but it is not clear whether all nine samples were used to formulate the results shown in their Figure 1.
    To investigate within-bullet heterogeneity (which would be central in debunking Guinn's conclusions), they chose four bullets from lot 6003 and took cut three slices through each (at the site of the original three samples), and from each slice took one sample each from the center, the edge, and in between. Thus they were checking cross-sectional heterogeneity, which shouldn't be large anyhow. They then seemed to have averaged the three outer samples (though in different positions along the bullet), the three central samples, and the three intermediate samples. I think that averaging the radial results is questionable. I think it would make more sense to compare the radial variations at each site along the bullet. In the end, however, it probably didn't make much difference, because they found practically no heterogeneity anywhere.
    Analyzing the samples. The authors took considerable pains to analyze the samples as similarly as possible to the way that Guinn did, except for using some minor advances in instruments, programs for resolving peaks, and reference materials. They seem to have measured the same four basic impurities (Sb, Ag, As, Cu). They give details about the irradiation, cooling, and counting scheme for the short-lived Ag, but not for the other three elements, which are longer-lived and require different conditions. I assume that was just another example of carelessness and lack of proofreading.
    They used three sets of standards (knowns). Their main one was solutions from the ICP world, which they dried inside the irradiation vials (Guinn's way). This shows the link to Pinkston and the earlier ICP-AES analyses. Another was a standard reference bullet lead. The third was the standard reference material orchard leaves (an oldie but a goodie). I see nothing to quibble about here, as they saw nothing to quibble about in Guinn's basic analyses. Thus their basic analytical methods are not in question.
    The paper discusses only the Sb and Ag data, the two elements that Guinn most depended on. Presumably the on-line supplemental material will show the results for the other elements.

Results
    Basic results for Sb. Here we briefly consider the new paper's basic results for Sb. We can ignore Ag because it has very little discriminatory power relative to Sb.
    The basic results are shown in their Figure 1, for each of the ten bullets in each of the three boxes. They are very different from what Guinn found. About the only similarity is the overall range of concentrations, from less than 50 ppm to 1800 or so.
    The big difference is "clumpiness." Lot 6000 has 6 of 10 values around 50 ppm. Lot 6003P has 8 of 10 values around 150 ppm. Lot 6003 has five of the ten samples in two smaller groups, around 1000 and 1700 ppm. Guinn's data showed nothing like these "preferred values."
    The authors used these groups to claim that there can be many more accidental matches in fragments than indicated by Guinn's data. At least one of the five assassination fragments in the two groups can now be an accidental match from that second MC rifle. In other words, there really were three or more groups (bullets) posing as two.
    The big problem with this argument is that their data show most of the matches at much lower concentrations than in the fragments. There are no matches near near the 600–800 ppm Sb of those fragments because there are virtually no concentrations there—only one of 30 bullets fell in that range. The authors gloss over this problem. On this omission alone, the basic thrust of their paper weakens to the point of failing. The authors might respond that matches at concentrations above and below those of the assassination fragment leave the door open for matches at the level of the assassination fragments, but they still have not shown such matches. Thus their prime argument remains speculative.
    The clumpiness was probably just the luck of the draw. It is the Achilles' Heel of this paper, however, because it almost certainly was responsible for the killer problem of lack of within-bullet heterogeneity discussed below. The clumpiness both invalidates this work and its authors' objections to Guinn's conclusions. The authors did not acknowledge that.
    An accidental match. Another example of this article's tendency to avoid full discussion is the accidental match that they found to an assassination fragment. At one point in the paper, they criticized the Sturdivan/Rahn estimate of 2%–3% for an accidental match with other MC bullets because it was based on the "too few" 14 test bullets used by Guinn. Shortly after that, however, they proclaimed that one of their bullets matched an assassination fragment. That is one match in 30 WCC/MC bullets (3%), just as we had predicted. No acknowledgment of that, either.
    The killer problem of within-bullet heterogeneity. WCC/MC bullets are notorious for their heterogeneity of Sb (within and between bullets). Guinn showed data on four samples from each of three test bullets that revealed a wide range of Sb in each. This was a great stumbling block to using the NAA results from the five assassination fragments to reveal the true number of bullets that hit. Eventually Larry Sturdivan and I overcame the problem, but it wasn't easy.
    Spiegelman et al. checked four of their bullets from lot 6003 for heterogeneity. The results, shown in their Table 3, gave essentially no heterogeneity for Sb (maybe a couple of percent, but that was around the level of their analytical uncertainty). Thus we have very large within-bullet heterogeneities from Guinn and none from the new paper. Spiegelman et al. did not address this qualitative difference in results, at least anywhere that I could find. All they said was that they could use the small heterogeneities in their statistics.
    There is a huge conceptual problem associated with finding large between-bullet heterogeneities and no within-bullet heterogeneities, because you can't have one without the other. The large variations between bullets, which represent heterogeneities within a vat of molten lead, must translate into large variations within some bullets, those drawn from the transition zones between different concentrations. Guinn found both kinds of heterogeneity, but these authors did not. This means that the new 30 bullets are unrepresentative of the larger population in ways that Guinn's bullets were not. Spiegelman et al.'s bullets are lacking an essential characteristic that Guinn's bullets showed.
    Conflict with previous article. The lack of heterogeneity also brings this paper into sharp conflict with the previous revisionist article (Randich and Grant, 2006). That paper proposed in detail that the large within-bullet heterogeneity in WCC/MC bullets was a natural result of segregation of certain elements, including Sb and Cu, near the boundaries of crystals of Pb as the molten lead cooled. This process, they said, could easily produce differences on the order of 200 ppm Sb in fragments, like those in the two groups from the assassination found by Guinn and the FBI. The trouble with this explanation, as pointed out in my review of that article, was that it required correlations between Sb and Cu that are not observed in WCC/MC lead. So much for that idea.
    Now come Spiegelman et al. finding no heterogeneity in their bullets. There is no way to reconcile these two revisionist articles on this point. The first gives a detailed explanation for heterogeneity; the second finds none of it. In effect, Randich and Tobin has become Randich vs. Tobin. The second article does not point out this conflict with the first, just as it did not note the conflict with Guinn's results.
    The Ronny Heindryckx Principle. This situation created by this article reminds me of the "Ronny Heindryckx Principle," a name I have given to the philosophy of a Belgian graduate student of analytical chemistry I knew in the early 1970s. Ronny said to me one day, in all seriousness, "I never repeat an experiment, because it will always give different results, and I won't know whether the first or second one was right. So I will have to do it a third time, and I don't want to do that." Guinn's data on 14 test bullets from all four lots gave a large range of Sb concentrations, a well-formed distribution of Sb concentrations, and major heterogeneities within bullets and between bullets. The repeat experiment (this paper), on 30 test bullets from two of the four lots, gave a similar range of concentrations but a clumpy distribution and no heterogeneity within bullets.
    Lacking a third experiment, we are thus limited to drawing conclusions from the first two. Which is right? Since there are no grounds for discrediting any of the actual analyses, everybody must be right. A full explanation must incorporate both sets of results.
    The full explanation should be something like this: The wide range of Sb concentration in WCC/MC lead was created by incomplete mixing of virgin lead (very low in Sb) and scrap lead (sometimes high in Sb). The manufacturer mixed the molten lead just enough to keep the Sb within specifications, not to truly homogenize the lead. This created pockets of higher Sb (clumpiness), which can sometimes be picked up by larger numbers of analyses. Evidently two of the three boxes of Spiegelman et al.'s bullets were drawn from pockets like this, whereas Guinn's samples were drawn from clumps and the surrounding lead.
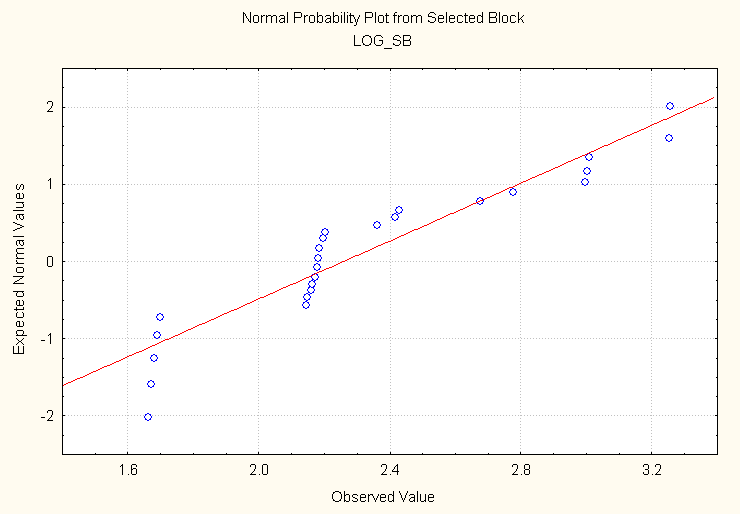
    But the clumpiness does not destroy the overall similarity of the two sets of bullets—it just provides fine structure. That important conclusion is shown in the graphic below. It is a normal probability plot for Spiegelman et al.'s 30 bullets. Since log(Sb) was used, it amounts to a log-normal probability plot. The fact that overall data follow the red straight line means that the values are distributed log-normally, just as Sturdivan/Rahn found for Guinn's test bullets (and the NRC report found for most other bullets). The clumpiness of some of the values is just superimposed on the log-normal distribution.

    Thus, in spite of the apparent big differences between these bullets and Guinn's, they are actually more similar than different.

Why no within-bullet heterogeneity?
    The last big question remaining is why the MC bullets of Spiegelman et al. did not show any within-bullet heterogeneity. As noted above, within-bullet heterogeneity must be found wherever there is great between-bullet heterogeneity. Guinn found it—why didn't Spiegelman et al.? Since Spiegelman et al. accepted the validity of Guinn's measurements, they implicitly accepted his heterogeneities. They experimentally confirmed his between-bullet heterogeneities, but not his within-bullet heterogeneities, and yet said nothing about that notable absence.
    The only answer is that the bullets of Spiegelman et al. were not representative of the full population. Perhaps it was because Spiegelman et al. only got bullets from two of the four lots. I doubt this, however, because Guinn's measurements showed that the lots shared the same basic properties. The only remaining explanation, assuming that Spiegelman et al. measured Sb properly, seems to be that their lack of heterogeneity is linked to the "clumpiness" of their Sb concentrations. Since they found two major differences in their samples, it would be logical to think that they might be related.
    Indeed, at least three of the four bullets used in the heterogeneity study come from obvious "clumps." If a clump represents a volume of lead with similar concentrations of Sb (because it has not been fully mixed with the surrounding lead), then it is reasonable to suppose that its homogeneity extends down to small sizes, i.e., that the clump possesses little or no detectable heterogeneity. The figure above shows that at least 28 of the 30 bullets belonged to such clumps, and so should have small degrees of heterogeneity. (Clumps are homogeneous, and these bullets were drawn from clumps.) That is exactly what Spiegelman et al. found. I think it is no coincidence. Spiegelman et al. were working with unusually clumped bullets that therefore showed unusually low heterogeneities. Guinn was working with bullets that were less clumpy and more heterogeneous. It may be as simple as that.

Implications for Spiegelman et al.'s conclusions
    Unfortunately for Spiegelman et al., the clumpiness and resulting homogeneity of their bullets greatly weaken the force of their conclusions. They can no longer claim that their results are general for WCC/MC bullets (through no fault of their own, I should add). The frequency of accidental matches they inferred was too high to be general, and the lack of representativeness they claimed for Guinn's bullets applies to theirs instead. Their claim that the five fragments from the assassination could have come from three (or more) bullets rather than two is all but destroyed by the unrepresentativeness of their bullets. The random matches they claimed were actually no more than a fluke of the unfortunate suites of bullets they analyzed. While the unrepresentativeness is not their fault, the overinterpretation throughout their paper definitely is. Its net effect is to confuse rather than to enlighten the ballistic aspects of the JFK assassination.

Summary and conclusions
    The authors' diligence in acquiring three boxes of WCC/MC bullets and analyzing 30 of them by neutron activation is commendable. Nonetheless, they produced a careless, sloppy paper that is difficult to read and full of basic errors. More importantly, the new bullets were clumpy in Sb and lacking the within-bullet heterogeneity that must accompany the large between-bullet heterogeneity that both they and Dr. Guinn found (and that are probably two sides of the same coin). This means that the new bullets did not represent the greater population of WCC/MC bullets in the ways that Guinn's had. Consequently, the new results cannot be generalized. In particular, the claim of significantly more-frequent accidental matches and the corresponding significantly higher probability of a second shooter cannot be supported. In this connection, it is ironic indeed that the new results revealed exactly the same frequency of accidental matches to the assassination fragments (3%) that Sturdivan and Rahn had predicted for WCC/MC lead. In the end, Guinn's results and conclusions remain unchallenged—the five assassination fragments were consistent with two and only two bullets, to a probability of at least 97%. In terms of the question in their title, the bullet fragments still say that a second shooter is possible only at a probability of 3% or less. The revisionist NAA studies are now 0 for 2.