
Answers to selected
problems, Chapter 11
Review questions
5. Which of these variables should affect the vapor pressure
of a liquid?
(a) Temperature? Yes, certainly, because the greater
the kinetic energy of the molecules in the liquid, the more of them will escape
through the surface.
(b) The volume of liquid at equilibrium? No, because
only the properties at the interface matter.
(c) The volume of vapor over the liquid at equilibrium?
No, for the same reason as (b).
(d) The area of the liquid's surface? No, again for
the same reason as (b).
12. (a) Do all phase diagrams (substances) have a critical
point? All substances that can exist as a liquid and a vapor have a critical
point.
(b) Do all phase diagrams have a normal boiling point?
Only those substances that can boil at one atmosphere do. Some substances cannot
boil at one atmosphere, even at very high temperatures. For example, CO2,
which sublimes (passes directly from solid to vapor), does not have a normal
boiling point.
(c) Can a phase diagram have more than one triple point?
Substances with more than one polymorphic solid form can have more than one
triple point. See the example of HgI2 given in the text.
Problems
27. This is an easy one. Table 11.1 shows that 27.4 kJ are required to vaporize one mole of CS2. Since one mole of CS2 is 76 g (actually 76.15 g), the heat per kg will be (27.4 kJ mol-1)/(76.15 g mol-1)(103 g/kg) = 360 kJ.
31. This is a two-step problem. The first step is to determine the amount of heat required to vaporize 0.750 L of water at 298 K. That is obtained from the heat of vaporization of water given in the problem:
H2O(l) —> H2O(g) ΔHvapn = 44.0 kJ
Remember that this is 44.0 kJ per
mole of water, or per 18 g of water. Since there are (750 g H2O)/(18
g mol-1 H2O) = 41.7 moles of water in this problem, the
total heat needed will be (44.0 kJ mol-1)(41.7 mol H2O) =
1830 kJ total.
The second step is to find out how much propane must be burned in order to
release this much heat. From the equation for burning propane,
C3H8 + 5 O2(g) —> 3 CO2(g) + 4 H2O(l) ΔH = -2.22x103 kJ
we see that 2220 kJ are released per mole of propane (44.1 g) burned. Thus, we need to burn (1830 kJ)/(2220 kJ mol-1 propane) = 0.83 mol propane. Since there are 44.1 g per mole of propane, we need to burn (0.83 mol propane)(44.1 g mol-1 propane) = 36.4 g propane.
35.

(a) The vapor pressure of CS2 at
30 °C is about 425–430 mmHg.
(b) The boiling point of ethanol at a pressure of 720 mmHg is
just the temperature at which its vapor pressure equals the ambient pressure.
You find the point where ethanol's curve crosses 720 mmHg and see what
temperature it corresponds to. The answer is about 76–77
°C.
41. This problem can be approached in two steps. First is to see
whether any of the water that is injected into the flask should freeze. Given
that the initial temperature is 30 °C, none will freeze (the easy part).
Next is to address how the water partitions itself between liquid and gas. Since
the water has a well-defined vapor pressure at this temperature, at least some
of it will be gaseous. But will all of it, or will most of it evaporate? To
answer this, you see whether its vapor pressure is high enough that all of it
could evaporate. The easiest way is to calculate the mass of vapor that would
fill the flask at the water's vapor pressure. If there is less water than that
value, it will all evaporate. If there is more that than, not all the water can
evaporate.
So now we use the ideal gas law in the form PV = nRT = (m/M)RT, which gives m =
PVM/RT = [(31.8 mmHg/760 mmHg atm-1)(2.55 L)(18 g mol-1)]/[(0.082 l
atm mol-1 K-1)(303 K) = 0.077 g H2O. But 1.82 g was injected, which
is far more than the 0.08 g needed for saturating the flask. Thus practically
all the water will remain as liquid. Let us say that of the 2550 mL of the
flask, roughly 2 mL will be condensed vapor (water) and the rest of the volume
will be filled with vapor.
For any of you who like algebra, try to solve exactly for the volume that will
be occupied by water. If you find the answer, tell us, because I haven't had a
chance to try it myself yet (6 Dec 99).
45. (a) Can a gas always be liquified by applying enough pressure? Not if its temperature is above its critical point. (See figure below.)
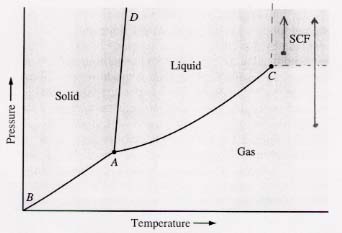
The arrow shows what happens when a gas (SCF in this case)
whose temperature is above the critical value is subjected to increasing
pressure—
the arrow just moves parallel to the border between SCF and liquid but does not
cross it.
Note how the same thing happens for an arrow starting below the SCF zone.
(b) Can a gas always be liquified by reducing the temperature enough? Strictly speaking, no, because sometimes the gas will be solidified rather than liquified. As long as the pressure of the gas is above that of its triple point, it can be liquified solely by reducing its temperature (the middle arrow in the diagram below). This result holds even for beginning with a supercrtical fluid (uper arrow below). But if the gas is at a pressure below the that of its triple point (lower arrow below), solely reducing the temperature will change it directly to a solid ("deposit" it), not liquify it.
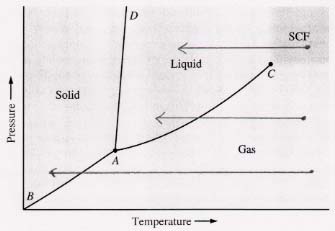
This diagram shows how a gas and an SCF can both be liquified and solidified solely by reducing the temperature.
(c) Can a gas always be liquified by increasing the pressure enough and reducing the temperature enough? Yes, even when it starts below the triple point. (See diagram below.)
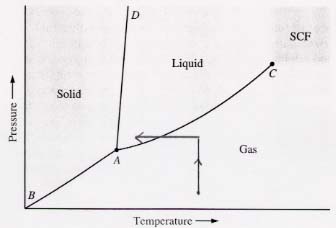
This diagram shows that a gas initially below the pressure
of the triple point can be liquified by increasing its pressure to
above the triple point and then reducing its temperature. The opposite sequence
of steps gives the same result.
47. Heat required to melt a block of ice. Table 11.4 shows that the heat of fusion of ice is 6.01 kJ per mole. So to find out how much heat is required to melt a given block of ice, you just determine its mass in moles, which you get by multiplying volume by density and dividing by the molecular weight of 18, and multiply that by the heat of fusion. The full formula is:
ΔH = nΔHfus = (ρV/18)(6.01 kJ mol-1) = 6.7 kJ
51. Which of these would require the greatest amount of heat?
(a) melting 3 moles of ice at 0°C; (b) evaporating 10
g H2O(l) at 298 K; (c) melting 2 moles of ice at 0°C and
heating the water to 10 °C; and (d) subliming 1 mole of ice at 0 °C.
Rough calculations
(a) (3 mol)(6 kJ mol-1) = 18 kJ
(b) (10 g/18 g mol-1)(44 kJ mol-1) = 24
kJ
(c) (2 mol)(6 kJ mol-1) + (2 mol)(0.075 kJ mol-1
°C-1)(10 °C) = 12 + 1.5 = 14 kJ
(d) (1 mol)(50 kJ mol-1) = 50 kJ.
Note the interesting result that the heat of melting is 6 kJ per mole, while the
heat of vaporizing is 44 kJ per mole, or several times higher. The latter comes
close to heats of reaction, derived from bond energies, which are tens to
hundreds of kilojoules per mole. This is because the act of vaporizing water
breaks hydrogen bonds between the molecules, whose energies are some 10% to 15%
of typical bond energies. Melting, by contrast, is a much more gentle activity,
which requires far less energy because it separates the molecules less than
boiling does.
53.
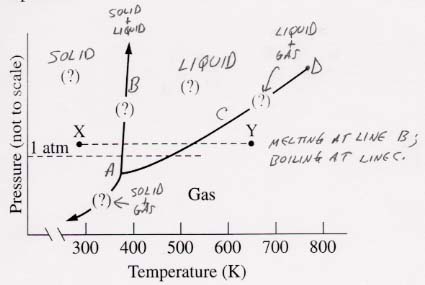
57.

It is very important to note that Figure 11.13 is REALLY not to scale. Therefore, the decisions about the zones that points A–D fall in cannot be made from the diagram. These points were put on the diagram after determining which zone they fell into.
(a) 88.15 °C and 0.954 atm pressure: The trick here is to recognize that at this temperature, the water can be only liquid or gaseous. If its vapor pressure exceeds 0.954 atm, the water will boil and be a gas. If not, it will be a liquid. From Table 11.2 on page 464, you can see that water's vapor pressure at 88 °C is about 500 mmHg, or about 0.66 atm, which is far less than the actual pressure of 0.954 atm. Thus the water is a liquid because it doesn't have enough vapor pressure to boil. To put it another way, the position of the boiling line (C) immediately below A is 0.66 atm.
(b) 25.0 °C and 0.0313 atm pressure: This question is sneaky. If you look at the vapor pressure of water at 25 °C in Table 11.2, you will see that it is 23.8 mmHg, which just happens to be 23.8/760 = 0.0313 atm! Thus B falls on the boiling line C, and both liquid and gas are present.
(c) 0 °C and 2.50 atm pressure: This is an easy one. Note from the form of the phase diagram that water is a liquid at 0 °C and all pressures above that of the triple point A. Thus our point C falls in the liquid zone.
(d) -10 °C and 0.100 atm pressure: At this low temperature and pressure, the water can be solid or gaseous. As with (a) the state depends on whether water's sublimation pressure exceeds 0.1 atm (gas) or falls below 0.1 atm (solid). How to find the sublimation pressure of water at -10 °C? There is no table in the book. Instead, you can see from the triple point, whose pressure is 4.6 mmHg (vapor pressure and sublimation pressure because vapor and solid exist at this point), that the sublimation pressure at -10 °C must be lower than this, or less than 4.58/760 = 0.006 atm. Since this pressure is far below the actual pressure of 0.1 atm, the ice cannot sublime to any significant extent, and will remain as ice (solid).
61. First, both substances have about the same molecular weights. Second, diethyl ether is polar, whereas pentane is nonpolar. This means that molecules of diethyl ether will be attracted to each other by forces between the dipoles of the C=O bond, but pentane will have no such forces. Thus, diethyl ether will require more energy to break loose its molecules from the solid matrix, i.e., will have a higher melting point than pentane will.
67. First, the two nonpolar substances Cl2 and CCl4 will have the lower melting points. Cl2, with a smaller molecular weight than CCl4, will have the lower melting point of the two. Of the polar substances CsCl and MgCl2, the latter will be harder to melt because its cation Mg is smaller and more highly charged than Cs. Thus the order of melting points will be Cl2 < CCl4 < CsCl < MgCl2. The actual melting points are -103 °C, -23 °C, 646 °C, and 708 °C.
69. Since 1-octanol (C8H17OH) has hydrogen bonds in addition to dispersive forces, whereas octane (C8H18) has no hydrogen bonds, octanol should have the stronger intermolecular forces and the greater surface tension.
73.

(a) In order to be a repeating unit, the selection must be able
to be placed end-to-end or side-to-side without leaving and gaps in the
structure. This can be done with the upper unit but not with the lower one.
(b) The number of hearts in the repeating unit is four on the corners divided by
four because of how they are shared, plus to inside that belong completely to
the unit. This is gives 4(1/4) + 2 = 3. The number of diamonds is four (on the
edges) divided by two, plus one inside the structure = 4(1/2) + 1 = 3. The
number of clubs is like the diamonds: 4(1/2) + 1 = 3.
79.
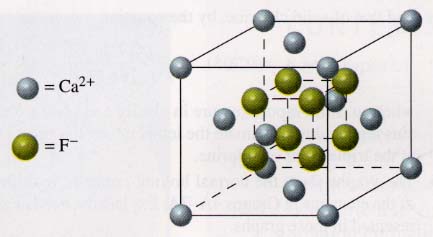
The number of calcium ions in this unit cell is eight at the
corners divided by eight cells each, plus six on the sides divided by two cells
each, or 8(1/8) + 6(1/2) = 4 Ca ions. The number of fluoride ions is eight (none
shared). Thus the empirical formula is Ca4F8, which is
equivalent to CaF2.
The coordination number (number of nearest neighbors) for the Ca ions is 8; for
F ions, 4.
81. The way to approach this problem is to follow the
nitrogen through the process and to realize that the volumes of the nitrogen and
of the benzene are both 172 mL even though they have different (partial)
pressures. So first you use a simplified version of the ideal gas law to
determine the (partial) pressure of the nitrogen in the final mixture. Then you
subtract this from the final pressure to get benzene's partial pressure.
Note that the temperature of the nitrogen gas does not change as it is passed
through the benzene. This allows us to use Boyle's law to calculate its final
pressure:
P1V1 = P2V2 —> P2 = P1V1/V2 = (750 mmHg)(150.0 mL/172 mL) = 654 mmHg
The partial pressure of benzene (its vapor pressure) is then 750 mmHg - 654 mmHg = 96 mmHg.
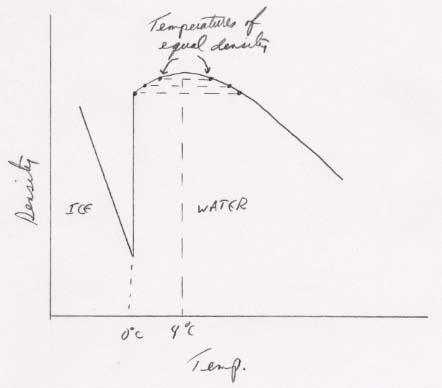
85. Because liquid water is most dense at 4 °C, each density between 0 °C and 4 °C will be matched by a density on the other side of 4 °C. The situation looks roughly like this:
89.

The upward slope of each of the four lines comes from dispersion forces (London forces) that increase with polarizability (roughly with size) of the molecules (or their central atoms). The anomalously high boiling points of H2O, HF, and NH3 stem from significant hydrogen bonding between their molecules.
93. First determine the pressure of the 1.00 g of water in
the flask at 35 °C and see if that pressure is less than the vapor pressure of
liquid water at that temperature. If it is, the water will remain as vapor. (It
is, so it does.) Then lower the temperature in the flask and find the highest
value at which the pressure exceeds the vapor pressure (at that new
temperature). That is the first point at which vapor will condense. You
may decrease the temperature so as to bracket the final temperature, or
you may work down progressively. The table below shows the results of the
progressive approach.
The easiest way to calculate the actual pressure of the water vapor is to
construct a formula with only the temperature and a constant. You can do that
easily from the ideal gas law:
PV = (m/M)RT —> P = (m/M)(R/V)T = (1 g/18 g mol-1)[(0.082 L atm mol-1 K-1)/(40 L)](TK) = 0.0866 TK
| T(C) | T(K) | Actual pressure, mmHg | Vapor pressure, mmHg | Condense? |
| 35 | 308 | 26.7 | 38 | NO |
| 30 | 303 | 26.2 | 31.8 | NO |
| 29 | 302 | 26.1 | 30.0 | NO |
| 28 | 301 | 26.0 | 28.3 | NO |
| 27 | 300 | 25.9 | 26.7 | NO |
| 26 | 299 | 25.8 | 25.2 | YES |
97. The different ionic structures of NaCl and CsCl are determined by the relative sizes of the ions. From page 338, we can read these ionic radii, all in picometers (pm): Na+ = 99, Cl- = 181, Cs+ = 169, Mg2+ = 65, and O2- = 140. Note how Cl- is about twice the size of Na+, whereas Cs+ and Cl- are about the same size. Since Mg2+ is about half the size of O2-, MgO will have the structure of NaCl rather than of CsCl. This structure is face-centered cubic. In MgO, the O2- ions will be at the corners and in the centers of the faces, as for Cl- in Figure 11.46 for NaCl.