Answers to selected problems, Chapter 2
Review questions
3. Literally, the problem asks for [OB/SB]/[OA/SA].
This equals [1.5/1.0]/[1.0/1.0], which is a complicated way of writing 1.5/1.0 =
1.5. But since the problem asks for a ratio of small whole numbers, we can just
multiply top and bottom by 2 to get 3.0/2.0 = 3/2.
10. Isotopes are atoms of the same element (i.e., having
the same Z) with different masses (i.e., different numbers of neutrons). Isobars
(page 41) are atoms of different elements but with the same masses.
(a) Isobars because masses are same (70) but elements are
different (Z = 33 and 34).
(b) Isotopes because Z is same (28) but A is different (57 and 66).
(c) Neither isotopes nor isobars because the two atoms are identical (Z = 74 and
A = 186).
(d) Neither, because both Z and A differ.
(e) Same as (d).
18. (a) Magnesium is a substance because it is an element.
(b) Methyl is not a substance because it is a prefix for an organic group (CH3).
(c) Chloride is not a substance because it is an anion (Cl-), which
can exist only in connection with a cation.
(d) Ammonia is a substance because it is a compound (NH3).
(e) Ammonium is not a substance because it is a cation (NH4+)
and exists only with an anion.
(f) Ethane is a substance because it is an organic compound (CH3CH3).
Thus, only a, d, and f could exist in containers on a storeroom shelf.
25. (a) Because nearly all compounds that contain C are organic,
a molecular formula is usually sufficient.
(b) Since hydrocarbons contain only H and C (by definition), a molecular formula
is sufficient.
(c) Alcohols require structural formulas because they they must contain -OH
groups.
(d) Since alkanes contain on C and H, and with 2n + 2 hydrogens for each carbon,
a molecular formula is sufficient.
(e) Since a carboxylic acid must have a COOH group, it requires a structural
formula.
Problems
27. The results are consistent with conservation of mass because
the final mass of the system (0.608 g of ZnS + 0.592 g Zn = 1.200 g Zn and S)
equals the initial mass of the system (1.000 g Zn + 0.200 g S = 1.200 g Zn and
S). Note that the question asks whether the results are consistent with
the law of conservation of mass, not whether they prove it. There is a big
difference.
31. One forms the mass ratios of S and SO2 for the
two experiments and equates them:
[0.312 g S/0.623 g SO2] =
[1.305 g S/X g SO2]. X = 2.61 g SO2.
37. Numbers of protons and neutrons.
(a) 62Zn has 30 protons just because it is zinc (Z = 30 in the
periodic table). Since its atomic weight is 62, its number of neutrons is then
62-30 = 32.
(b) 241Pu has Z = 94. Thus if A = 241, it must have 241 - 94 = 147
neutrons.
(c) and (d) are done in the same way.
43. As explained and illustrated in the text, the weighted-average atomic mass of an element is just the sum of the products of the masses of each of its nuclides and their fractional abundances. For gallium this is (68.926 u)(0.601) [for gallium-69] + (70.925 u)(0.399) [for gallium-71] = 69.72, which rounds off at three significant figures to 69.7 u.
47. A slightly different twist on the same equation as in problem 43. Since the fractional abundances are not given, express them as x and 1.000 - x, which of course sum to the required 1.000 (100%). It doesn't matter which isotope of rubidium you assume to have abundance x. (If you don't believe this, try it both ways.) The equation then becomes (84.91179 u)(x) + (86.90919 u)(1 - x) = 85.4678. (This latter value is the overall atomic mass of Rb, as given in "The Elements" inside the front cover. By simple algebra, this becomes 84.91179x + 86.90919 - 86.90919x = 85.4678, or 86.90919x - 84.91179x = 86.90919 - 85.4678. It follows that 1.99740x = 1.4414, or x = 0.72164 (five significant figures). Thus, the abundance of rubidium-85 is 0.72164, and the abundance of rubidium-87 is 0.27836.
49. Easy.
51. The key point here is to recognize that the normal state of each of these elements is a diatomic gas: O2, Br2, H2, and N2.
53. Binary molecular compounds. Remember that the two elements
in binary molecular compounds are usually not metals (nonmetals and metalloids).
When you see a compound that contains a metal, the compound will usually be
ionic.
(a) HCN can't be a binary molecular compound because it isn't binary--it's
ternary (look it up).
(b) ICl is a binary molecular compound because it is composed of two nonmetals
(from Group VII).
(c) KI is binary but ionic because K is a metal.
(d) H2O is binary and molecular because both its elements are
nonmetals. (Recall that hydrogen is an exception within Group I.)
(e) ONF is composed of nonmetals but is ternary
59. Easy-straight from the book. You must learn each of these common chemical names.
61. Easy rule for naming binary ionic compounds: first element
(the metal) plus the second elements as -ide. When dealing with
polyatomic ions, you pretty much have to remember them. The link to the relative
number of oxygen atoms, given at the bottom of page 55, often helps. I suggest
that you put in yoiur time and learn the common polyatomic ions in Table 2.4. It
will help you in the long run. Here are some of the trickier names:
(c) FeCl2 is iron(II) chloride because iron can have oxidation states
of +2 or +3.
(i) Cr2(SO4)3 is chromium(III) sulfate because
chromium can have oxidation states of +3 or +6.
(m) Cu(OH)2 is copper(II) hydroxide because copper can have oxidation
states of +1 or +2.
(o) FePO4·2H2O is iron(IIII) phosphate
dihydrate because iron can
have oxidation states of +2 or +3 and because two waters of hydration are bound
here.
67. Again straight from the book.
69. Condensed structural formulas:
(a) pentane (five carbons in a straight chain) is CH3(CH2)3CH3.
(b) butanoic acid (organic acid with four-carbon chain) is CH3(CH2)2COOH.
(c) diethylamine (ammonia with ethyl groups substituted for two of the three
hydrogens) is (CH3CH2)2NH.
(d) cyclobutane (saturated four-carbon ring) has a square as its condensed
structural formula.
73. Isomers are molecules with the same atoms but in different
structures. The molecule here can be simplified to C7H16O.
(a) C7H16O = isomer.
(b) C7H16O = isomer.
(c) same as (b) but shown in reversed order.
(d) C8H18O = not an isomer.
79. The longest chain has five carbons. Since all the carbons
have four single bonds, the molecule is a pentane. From left to right, the
second carbon has two methyl groups in place of two of the hydrogens, and the
fourth carbon has one methyl group. That makes the compound
2,2,4-trimethylpentane (one long word).
(a) is (straight-chain) octane. (b) is 2,2,4-trimethylpentane. (c) has only
seven carbons. (d) has nine carbons.
Additional problems
81. Mass before the reaction: 10.00 g CaCO3 + (100.0
mL HCl)(1.148 g mL-1) = 10.00 g + 114.8 g = 124.8 g.
Mass after the reaction = 120.40 g solution + (2220 mL CO2)(0.0019769
g mL-1) = 120.4 g + 4.3887 g = 124.8 g.
Since the two masses are indistinguishable within experimental error, mass may
be said to have been conserved (mass is not not conserved).
87. The two proportions of Fe and O will have to be in the
ratios of two small whole numbers. Convert the proportions of the original
compound and each of the four possible second compounds to Fe/O and see which of
the candidates is properly related to the first compound.
The mass ratio Fe/O for the first compound is (1.0000 - 0.2236)/0.2236 =
0.7764/0.2236 = 3.472 (to four significant figures). The Fe/O ratios for the
four other compounds, calculated in the same way, are (a) 2.618, (b) 1.236, (c)
1.0000, and (d) 0.4908. The ratios of these values to the original 3.472 are (a)
0.7540, (b) 0.3560, (c) 0.2880, and (d) 0.1414. Only the first of these new
ratios, 0.7540, resembles a ratio of small whole numbers (3/4). Thus compound
(a) is the right answer.
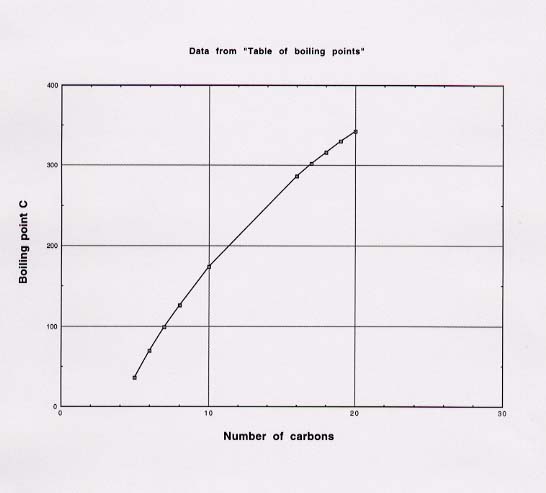
93. The real way to estimate the boiling points of various alkanes is to plot the known boiling points versus the number of carbons in the straight chain (with number of carbons as the independent variable) and read the unknown boiling points from the plot. A plot like this can be made by hand or with any of several graphical packages for the computer. The unknown boiling points can also be estimated by interpolating between two of the known values of extrapolating from two known values. The relative merits of the two approaches will depend on which pairs of values are closer to the desired unknown.
Interpolating
For the C11 alkane, you could interpolate between octane (eight
carbons) which boils at 125.7 ºC (page 66), and the C16 alkane,
which boils at 286.79 ºC (from this problem). The 11-carbon alkane is 3/8 of
the way from 8 carbons to 16 carbons, so we can estimate its boiling point to be
3/8 of the way from the first boiling point to the second. The whole
"way" is 286.79 ºC - 125.7 ºC = 161.1 ºC. Three-eighths of this is
53.0 ºC, or 125.7 + 53.0 = 178.7 ºC.
Extrapolating
Since Example 2.13 on page 66 gives the boiling points for C5 through
C10 alkanes, and we want the value for C11, we will be
more accurate if we use these values. From the table on page 66, you can see
that from C5 to C10, the boiling points increase by 32.6
ºC, 29.7 °C, 27.3 °C, 25 °C, and 23 °C (the last two values being
approximations). So to estimate the value for for C11, just take the
value for C10 and add a bit less than 23 °C. If you add 22 ºC to
the value for C10, you would get 174 °C + 22 °C = 196 °C.
The other boiling points can be estimated analogously.
Here is a plot of boiling points vs. number of carbon atoms.
