Answers to selected problems, Chapter 6

Review questions
19. Equations for standard enthalpies of formation must always be written for one mole of the substance in question. Whereas we would usually write the balanced equation of formation for Fe₂O₃ as 4 Fe(s) + 3 O₂(g) ® 2 Fe₂O₃(s) (to avoid a fractional coefficient for O₂), for the purposes of enthalpy we must write it as 2 Fe(s) + 1.5 O₂(g) ® Fe₂O₃(s).

21. H₂(g) gets a standard enthalpy of formation of zero because it is the elemental state of hydrogen. H⁺(aq) gets a standard enthalpy of formation of zero because it serves as the reference point for other ions (by convention).

Problems
25. Change in internal energy = (energy in) - (energy out) = 455 J - 325 J = 130 J.

31. The reaction is endothermic because it requires energy to make it go, that is, it absorbs energy. In other words, it is not spontaneous.
        q = (134 kJ/10 g H₂O)(18 g H₂O/mol H₂O) = 241 kJ/ mol H₂O. This q is enthalpy, DH, because the problem specifies that the reaction proceeds at constant pressure rather than at constant volume. In this sense, it is like most of the reactions in the real world.

35. We start with the reaction 3 Fe₂O₃(s) + CO(g) ® 2 Fe₃O₄(s) + CO₂(g)   DH = -46 kJ
        (a) The reaction Fe₂O₃(s) + 1/3 CO(g) ® 2/3 Fe₃O₄(s) + 1/3 CO₂(g) is 1/3 of the initial one, so its change in enthalpy is 1/3 of the first, or -15.3 kJ. (See bottom of page 241 and top of 242.)
        (b) The reaction Fe₃O₄(s) + 1/2 CO₂(g) ® 3/2 Fe₂O₃(s) + 1/2 CO(g) is 1/2 the opposite of the first one, so its change in enthalpy is -1/2 of that one's, or 23 kJ.

39. Given the reaction to make calcium hydroxide: CaO(s) + H₂O(l) ®  Ca(OH)₂(s)  DH = -65.2 kJ. Remember that the value of DH cited always refers to one "mole" of the reaction, or 56 g of CaO, 18 g of H₂O, etc.  The problem says that 0.500 kg CaO will be used, which corresponds to (500. g)/(56 g/mol) = 8.93 mol CaO. Thus the change in enthalpy will be (8.93 mol CaO)(-65.2 kJ/mol CaO) = -582 kJ, or 582 kJ given off.

45. The trick here is to recognize that you can only determine the actual DH of the second equation when you know how many moles of methane are being oxidized, because the reaction as written refers to 1 mole of methane. So you use the ideal gas law to solve for n and adjust the change in enthalpy to this number of moles. Then you apply that answer to the first equation and find the number of moles of CaO required, again by scaling. Lastly, convert that number of moles to grams of CaO.
        (a) Find the number of moles of CH₄ in 1.090 L, 772 Torr, and 21.5 °C. n = PV/RT = [772 Torr/(760 Torr/atm)](1.00 L)/[(0.0821 L atm mol^-1 K^-1)(273 °C+ 25 °C)] = 0.04152 mol CH₄.
        (b) Find the actual change in enthalpy of the second reaction for 0.04152 mol CH₄. (-890.3 kJ/mol CH₄)(0.04152 mol CH₄) = -36.96 kJ per 0.04152 mol CH₄.
        (c) Find the number of moles of the first reaction needed to liberate 36.96 kJ. 1 mole of the reaction is to -65.2 kJ as x moles of the reaction is to -36.96 kJ. This is equivalent to 1/x = -65.2/-36.96, or x = 0.567 mol reaction.
        (d) Find the number of grams of CaO in 0.567 mol. (0.567 mol CaO)(56 g CaO/mol CaO) = 31.7 g CaO needed. (The official answer is 32.2 g; the differences come from using exact temperatures and atomic weights.)

49. The heat capacity of the piece of iron is just the heat required to raise its temperature by 1 °C (from q = CDT). This is 112 J/27 °C = 4.1 J/°C.

57. Solve this problem by equating the heat lost by the iron to that gained by the water and noting that the final temperatures of iron and water will be the same. As always, set up the problem algebraically first. C_FeDT_Fe = C_H2ODT_H2O. This becomes (M_Fe)(Specific heat Fe)(DT_Fe) = (M_H2O)(Specific heat H₂O)(DT_H2O). This in turn becomes (M_Fe)(Specific heat Fe)(T_Fe - 39.6 °C) = (M_H2O)(Specific heat H₂O)(39.6 °C - 23.3 °C). Now just solve for T_Fe. 
T_Fe - 39.6 °C = [(M_H2O)(Specific heat H₂O)(39.6 °C - 23.3 °C)]/[(M_Fe)(Specific heat Fe)] 
= [(817 g)(4.182 J g^-1 °C^-1)(16.3 °C)]/[(1350 g)(0.449 J g^-1 °C^-1)] 
= 91.88 °C = T_Fe - 39.6 °C
T_Fe = 131.5 °C.

61. Remembering that DH is written for one mole of reactants (because all coefficients in the equations are unity), the steps to solve this problem are (1) determine the total heat given off in the calorimeter, and (2) expressing this per mole of reactants.
    (1) The total heat released by the reaction is q cal = (m_water g)(specific heat_water)(DT_water) = (1000 mL)(1.000 g mL^-1)(4.18 J g^-1 °C^-1)(23.21 °C - 20.00 °C) = 13,418 J.
    (2) Total moles of reactants = (0.5000 L)(0.500 M NaOH) = 0.250 mol NaOH and (0.5000 L)(0.500 M HCl) = 0.250 mol HCl. Thus the heat given off per mole is 13.418 kJ/0.250 mol = 53.7 kJ mol^-1. This makes DH = -53.7 kJ mol-1. The final equation for the reaction would thus be written:
    HCl(aq) + NaOH(aq) ® NaCl(aq) + H2O(l)  DH = -53.7 kJ

65. The steps here are: (1) Determine the total energy given off by the reaction to the calorimeter; (2) Divide by the number of grams of coal burned.
    (1) Total energy given off = heat capacity of calorimeter x change in temperature of calorimeter = (4.62 kJ °C^-1)(22.28 °C - 20.45 °C) = (4.62 kJ °C^-1)(1.83 °C)  = 8.45 kJ.
    (2) -8.45 kJ/0.309 g = -27.4 kJ g^-1 coal.

71. To solve this problem, you reverse the second equation and add it to the first:

    (Reversed second)        2 NO₂(g)           ® N₂(g) + 2 O₂(g)   DH = -33.2 kJ
    (First)                            N₂(g) + 2 O₂(g) ® N₂O₄(g)                DH = +9.2 kJ
    (Sum)                           2 NO₂(g)            ®  N₂O₄(g)               DH = -24.0 kJ

    Note how according to Hess's law, reversing the equation changes the sign of DH.

75. This problem is just like the previous one, except with one more equation. So that you can follow my logic, here are the three starting equations and the final equation:

Starting:
    N₂(g) + 3 H₂(g) ® 2 NH₃(g)
    N₂(g) + O₂(g)    ® 2 NO(g)
    2 H₂(g) + O₂(g) ® 2 H₂O(l)

Final:
    4 NH₃(g) + 5 O₂(g) ® 4 NO(g) + 6 H₂O(l)

    The approach here is the same as with balancing equations: find terms in the final equation that appear in only one of the starting equations and see how the starting equation needs to be multiplied to match the final equation. If that approach doesn't cover all the starting equations, work with the others first and look to the last step to see what multiple of the other starting equations is needed.
    The first equation is the only one with NH₃. Because the final equation contains twice any many NH₃'s as the first, and on the other side, multiply the first equation by -2.
    The second equation is the only one with NO. The final equation contains twice as many NO's as the first, and on the same side. Therefore, multiple the first equation by 2.
    (You confirm that the second equation must be handled oppositely to the first because both contain 1 N₂ on their left sides, which must cancel because N2 appears in neither the third equation nor the final one.)
    The third equation is the only starting equation to contain H₂O. The final equation contains three times as many H₂O's, and on the same side. Therefore, multiply the third equation by 3.

    Here are the multiplied starting equations and the final equation, with terms cancelled out as appropriate:

    4 NH₃(g)              ® 2 N₂(g) + 6 H₂(g)
    2 N₂(g) + 2 O₂(g) ® 4 NO(g)
    6 H₂(g) + 3 O₂(g) ® 6 H₂O(l)
   4 NH₃(g) + 5 O₂(g) ® 4 NO(g) + 6 H₂O(l)

    Treating the changes in enthalpy with the same coefficients gives -2(-92.22 kJ) + 2(180.5 kJ) + 3(-571.6 kJ) = -1169.4 kJ = -1169 kJ.

77. To calculate the standard enthalpy change for each reaction, just add the standard values for the substances of the left and subtract those on the right. (See pages 256 ff. in the text.) Of course, some of the values may in general have to be multiplied by small integer factors that are needed to create the final reaction from its component reactions (as shown in the previous problem), but that is not needed here because of the simple reactions involved. (Problem 78 needs this approach, however.)
    (a) DH°  = DH_f° [NH₄Cl(s)] - DH_f° [NH₃(g)] - DH_f° [HCl(g)] = (-314.4) - (-46.11) - (-92.31) = -176.0 kJ
    (b), (c), and (d) are done similarly.

83. As in problem 77, DH°  = DH_f° [NH₃(g)] + DH_f° [H₂O(l)] - DH_f° [NH₃⁺(aq)] - DH_f° [OH^-(aq)] = 46.11 kJ + (-285.8 kJ) - (-132.5 kJ) - (-230.0 kJ) = 30.6 kJ.

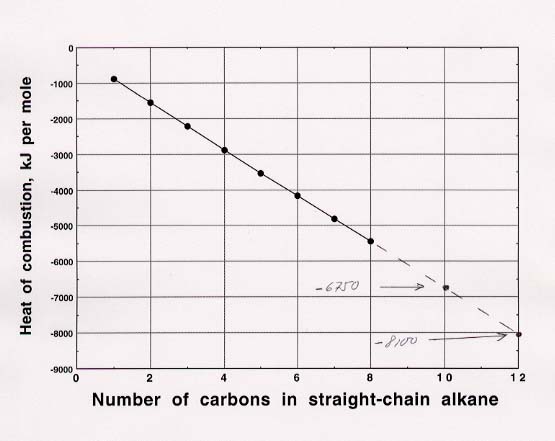
85. (a) I have prepared two plots, one for the heats of combustion per mole of compound and the other for heats of combustion per mole of C (what the problem actually requested).

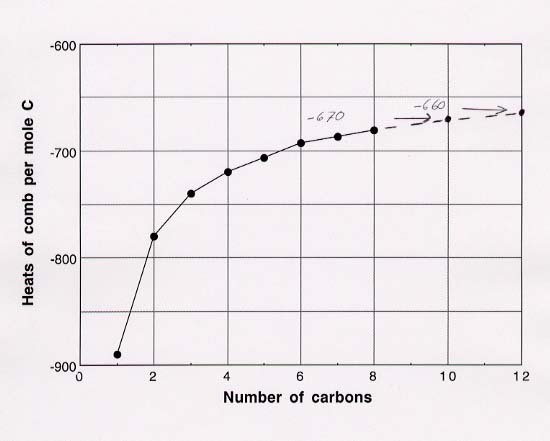
      (b) Estimates of heats of combustion can be read directly from the first plot: -6750 kJ per mole for decane and -8100 kJ per mole for dodecane. Estimates from second plot, which will be more reliable because they essentially deal with differences from one point to the next, are obtained by multiplying the heat per mole of carbon by the number of moles of carbon: -670 kJ x 10 moles carbon per mole of substance = -6700 kJ per mole for decane and -660 x 12 moles per mole of substance  = -7900 for dodecane. It is possible to get results that are slightly more accurate by extrapolating mathematically rather than by reading directly from the plots, but we won't bother with that here.

91. (a) That his bride was watching in wonderment, realizing for the first time what a total nerd she had married!
      (b) Seriously, Joule could have foreseen two effects on the temperature of the falling water: a slight warming when the water hit bottom, as its kinetic energy is degraded to heat, and a slight cooling of the water by evaporation as it was falling. These two small effects would have made smaller to the extent that they cancelled one another. With Joule's bride looking over his shoulder, he probably was in no position to observe small effects like these, and he would have observed no change in temperature. This of course would have angered his bride still more, and she might have said something like, "James, dear, if you are going to leave me on our honeymoon for some dumb temperature under a waterfall, you can at least find some sort of change!" (His bride didn't appreciate that no change is just as significant a result as a change.)
        (c) There is, of course, a third possibility, one that all PC folks will appreciate, namely that Joule married a scientist and that she encouraged him to check the temperature at the bottom of the waterfall. Maybe it was even her idea!

97. The basic equation is CH₄(g) + 2 O₂(g) ® CO₂(g) + 2 H₂O  DH = -890.3 kJ.
       (a) To determine how much mass of CH₄(g) must be burned to give off 1.00x10⁵ kJ, you divide this number by 890.3 kJ per mole of CH₄(g), and get 112.3 moles of CH₄. You then multiply this by the molecular mass of CH₄, 16 g/mol, and get 1797 g of CH₄.
    (b) For this part, you must first find how many moles of CH₄ are contained in 105 L at 23 °C and 746 mmHg. That is a simple application of the ideal gas law: n = PV/RT = (746 mmHg/760 mmHg atm^-1)(105 L)/[(0.0821 L atm mol^-1 K^-1)(298 K)] = 4.21 mol CH₄. Next, scale the equation to this number of moles:
    (1 mol CH₄/4.21 mol CH₄)/(890.3 kJ/x kJ) ® x = (4.21)(890.3) = 3750 kJ.

103.   

Back to CHM101 Fall 2001
Back to Home Page