Failed Prediction About Variability Vs. Size Of Fragments
Perhaps the biggest failing of the metallurgical
explanation is its seriously wrong prediction for variations as a function of
fragment size. The article contains this prediction, but not explicitly.
The metallurgical picture predicts that the smaller the fragments, the more they will vary in
antimony (because the variations are purportedly caused by "microsegregation,"
or differences within grains). Small fragments can come from different places
within a grain, whereas larger fragments will span multiple grains and thus
average out the differences within grains.
Here are the article's actual sentences to this effect:
General statement: "…
if the sample size of a lead specimen approaches the grain size [i.e.,
decreasing—KAR], and the
antimony and copper trace elements are segregated at the boundaries, then the
variability of sample compositions will increase [as fragment size decreases—KAR]."
Statements for small fragments: (a) "However, if the samples
are only the size of, e.g., one to three grains, then each sample will likely
contain different relative proportions of grain-boundary and interior grain
material. This situation can result in increased compositional variability among
ostensibly equivalent samples." (b) "Certainly, 5–10
mg samples should be suspect with respect to being representative of the bulk
composition."
Statement for larger fragments: "…
if all samples were large enough to contain on the order of 50 or more grains [meaning
grain as crystal of lead, not unit of weight—KAR],
they will encompass a good average quantity of both grain-boundary material and
interior grain material and will be reasonably representative of the true
average composition of the alloy."
So the prediction is clear—as
fragments (samples) progress from larger to smaller, the variability of their
antimony (and other minor elements) will increase. The problem is that actual
measurements on WCC/MC lead show exactly the opposite—the variability of
antimony decreases as fragments progress from larger to smaller.
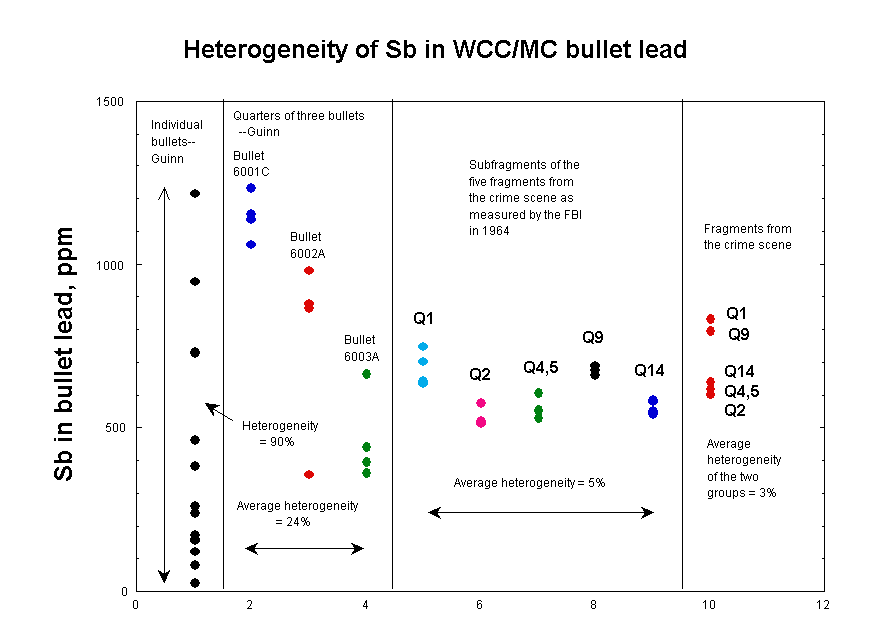
This clear trend can be shown on a figure that I prepared
some years ago and that was well known to the authors of this article.
Larry Sturdivan and I also included it as Figure 2 in the first of our two
articles from 2004.

The largest sizes, represented by samples from Guinn's 14
individual bullets, have a heterogeneity (standard deviation) of 90% for
antimony. At the next-smaller scale, represented by the three individual bullets
used for quarter-bullet studies, the heterogeneity was 40% (figure not shown in
plot). Within each of the three bullets, the heterogeneity averaged 24%. Within
the FBI's replicate analyses of the five fragments from the crime scene, it was
a mere 5%. Within the two groups of fragments from the crime scene, it averaged
3%, which is just about the analytical uncertainties.
Summarized in tabular form, the results look like this:
| Size scale | Heterogeneity, % |
| 14 test bullets | 90 |
| Three test bullets | 41 |
| Within three test bullets | 24 |
| Within FBI replicates | 5 |
| Within two JFK groups | 3 |
| Estimated anal. uncert. | 6 |
In other words, the measured heterogeneities decreased from 90% from bullet to bullet down to <6% (i.e., unmeasurable) for the tiniest fragments. Since the article's metallurgical explanation predicted the opposite, it is clear that the explanation is wrong.
Possible alternative view
It is possible to view the question of variations in an
entirely different light, however. This section attempts to give the article's metallurgical
standpoint its due. If you start by accepting that that grain-size
variations control the variations of copper and antimony in all the WCC/MC
samples, there would be no need to carefully consider their variations in the 14
test bullets and the 12 quarter-bullet samples. All the variations would just be
random noise, and so you would never have to consider things like the lack of
covariation and the opposite trends of variability with size than are predicted
by your theory.
But I don't think that is good enough. The quarter-bullet
data were there in plain sight all the time. Any argument that purports to explain all
the data needs to consider ALL the data. This paper, however, missed the critical—and
fatal to its theory—variations of antimony in the
three bullets that were used for the quarter-bullet samples. One bullet was
systematically lower in antimony than were the other two bullets, one was
intermediate in concentration, and the last was systematically the lowest in
concentration. Grain-size variations alone cannot explain that pattern—something
else had to be at work. (See the section "Do We
Really Need To Know Metallurgy?" for a few more comments on this critical
scale of variation.)
Thus this alternative point of view cannot justify overlooking this
significant piece of data against it.