16. Lurch 1 Angular—with bullet, head, and cloud
The model and its justification
Motions are of two basic types—translational
and rotational. Although every beginning physics students finds the
translational version more intuitive than the rotational, we really should be
using the rotational here. That is easy to justify, for the immediate effect of
the head shot was to rotate JFK's head forward about his neck, and the later
effect was to rotate his upper torso rearward about his hips. In other
words, JFK rotated rather than translated. We began with the translational
version simply because it is easier to understand. In truth, it should not be
used to address his motions after the head shot.
The basic rotational parameters are analogous to the
translational parameters, as shown in the table below:
| Parameter | Translational | Rotational |
| Momentum | p = mv | Ω = mvL/3 |
| Kinetic energy | KE = 0.5mv2 | KE = 0.5mv2fI/3 |
where L = lever arm (length of the rotating body in this case), v
is the speed at the outer end of the rotating object (the top of Kennedy's head,
for example), and fI is a geometrical factor having to do with
the shape of the object that is rotating (fI is 1.11 for a
rotating rod).
Lurch 1 Angular is the rotational analog of Lurch 1 Linear.
It is the rotational procedure for
calculating the speed of the rearward lurch of upper body from only the bullet, the body, and
the diffuse
cloud of fragments. You just write the rotational versions of the equations of
conservation, which are very similar to the translational versions, and solve
them in the same way. Recall that each term in the conservation equations
below has an L in the numerator, but that it has been eliminated because they
all cancel.
Solving the simultaneous equations
The rotational equations of conservation are shown
below. Note how similar they are to the translational versions in Lurch 1
Linear. The answer for vbodyafter comes out 35%
greater in magnitude than in the linear case —
-2.9 ft s-1
vs. -2.2 ft s-1. Recall that the actual initial lurch was 0.5–1.0
ft s-1 rearward This confirms that these simple translational and
rotational equations are off.
![]()
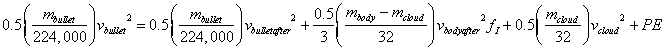
Default values of variables
| mbullet = 161 gr | vbullet = 1800 ft s-1 |
| mbody = 85 lb | vbulletafter = 200 ft s-1 |
| mcloud = 0.3 lb | PE = 300 ft-lb |
| Q = 12° | fI = 1.11 |
vbodyafter = -2.92 ft s-1 vcloud = 425 ft s-1
| Momentum | Energy, ft-lb | ||
| Before | After | Before | After |
| Ωbullet = 3.80 | Ωbulletafter = 0.43 | KEbullet = 1164 | KEbulletafter = 14 |
| Ωbodyafter = -8.58 | KEbodyafter = 4 | ||
| Ωcloud = 11.95 | KEcloud = 846 | ||
| PE = 300 | |||
Sensitivity analysis
The sensitivity analysis for Lurch 1 Angular is very
similar to that of Lurch 1 Linear. The most important variable is mcloud,
followed at a distance by mbody and PE. The other five variables are much
less significant, and don't have to be known particularly well.
Sensitivity tests, Lurch 1 angular
(Standard conditions in boldface)
|
mbullet |
vlurch |
mbody |
vlurch |
mcloud |
vlurch |
vbullet |
vlurch |
vbulletafter |
vlurch |
|
156 |
-2.870 |
|
|
|
|
1750 |
-2.801 |
|
|
|
157 |
-2.880 |
65 |
-3.820 |
|
|
1760 |
-2.825 |
0 |
-2.809 |
|
158 |
-2.891 |
70 |
-3.547 |
|
|
1770 |
-2.849 |
50 |
-2.844 |
|
159 |
-2.901 |
75 |
-3.310 |
0.1 |
-1.204 |
1780 |
-2.873 |
100 |
-2.874 |
|
160 |
-2.911 |
80 |
-3.104 |
0.2 |
-2.176 |
1790 |
-2.897 |
150 |
-2.900 |
|
161 |
-2.921 |
85 |
-2.921 |
0.3 |
-2.921 |
1800 |
-2.921 |
200 |
-2.921 |
|
162 |
-2.931 |
90 |
-2.759 |
0.4 |
-3.549 |
1810 |
-2.945 |
250 |
-2.938 |
|
163 |
-2.941 |
95 |
-2.613 |
0.5 |
-4.101 |
1820 |
-2.968 |
300 |
-2.951 |
|
164 |
-2.951 |
100 |
-2.483 |
0.6 |
-4.601 |
1830 |
-2.992 |
350 |
-2.959 |
|
165 |
-2.960 |
105 |
-2.365 |
0.7 |
-5.059 |
1840 |
-3.015 |
400 |
-2.962 |
|
166 |
-2.970 |
|
|
0.8 |
-5.486 |
1850 |
-3.039 |
|
|
|
Sensitivity = |
Sensitivity = |
Sensitivity = |
Sensitivity = |
Sensitivity = |
|||||
|
Range = 0.10 |
Range = 1.46 |
Range = 4.28 |
Range = 0.24 |
Range = 0.15 |
|||||
|
PE |
vlurch |
Q |
vlurch |
fI |
vlurch |
|
0 |
-3.583 |
|
|
|
|
|
50 |
-3.479 |
7 |
-2.902 |
1.06 |
-3.058 |
|
100 |
-3.373 |
8 |
-2.905 |
1.07 |
-3.030 |
|
150 |
-3.265 |
9 |
-2.908 |
1.08 |
-3.002 |
|
200 |
-3.153 |
10 |
-2.912 |
1.09 |
-2.974 |
|
250 |
-3.039 |
11 |
-2.916 |
1.10 |
-2.947 |
|
300 |
-2.921 |
12 |
-2.921 |
1.11 |
-2.921 |
|
350 |
-2.800 |
13 |
-2.926 |
1.12 |
-2.895 |
|
400 |
-2.675 |
14 |
-2.931 |
1.13 |
-2.869 |
|
450 |
-2.545 |
15 |
-2.937 |
1.14 |
-2.844 |
|
500 |
-2.411 |
16 |
-2.943 |
1.15 |
-2.820 |
|
550 |
-2.272 |
17 |
-2.950 |
1.16 |
-2.795 |
|
600 |
-2.127 |
|
|
|
|
|
Sensitivity = |
Sensitivity = |
Sensitivity = |
|||
|
Range = 1.46 |
Range = 0.05 |
Range = 0.26 |
|||
Ordered summary of sensitivities
| Variable | Sensitivity of vlurch | Range of vlurch, ft s-1 | Magnitude |
| Positive effect on lurch (reduces rearward velocity) | |||
| fI | 0.99 | 0.26 | Small |
| PE | 0.24 | 1.46 | Large |
| mbody | 1.00 | 1.46 | Large |
| Negative effect on lurch (increases rearward velocity) | |||
| Q | -0.02 | 0.05 | Small |
| mbullet | -0.55 | 0.10 | Small |
| vbulletafter | -0.03 | 0.15 | Small |
| vbullet | -1.48 | 0.24 | Small |
| mcloud | -0.70 | 4.28 | Large |
As was the case with Lurch 1 Linear, most of the variables (5 of 8) act to intensify the lurch. By far the largest effect is from the intensifier mcloud. The sensitivities for most variables are the same as for Lurch 1 Linear, whereas the effects are greater.
Summary
Lurch 1 Angular is similar in most ways
to Lurch 1 Linear, except that it gives a rearward lurch that
is 35% faster than the linear version, which in turn is greater than the
observed. This means that Lurch 1 Angular is representing the physical
situation less faithfully than its linear analog. The sensitivities are also similar to Lurch 1 Linear,
with mcloud being by far the most important.
Back to Lurch 7 Linear
Ahead to Lurch 2 Angular
Back to Physics of the Head Shot