5. Variables and values
The simulations reported here involve 33 variables of time, space, mass, velocity, and energy. They and their values are listed in the table below. Each variable is discussed individually after that.
| Variable | Symbol | Default value | Range of values |
| Mass of bullet | mbullet | 161 gr | 156166 gr |
| Entrance velocity of bullet | vbullet | 1800 ft s-1 | 17501850 ft s-1 |
| Exit velocity of bullet | vbulletafter | 200 ft s-1 | 0400 ft s-1 |
| Angle of bullet above horizontal | Θ | 12° | 7°17° |
| Mass of head | mhead | 7 lb | 410 lb |
| Mass of upper torso | mbody | 85 lb | 65105 lb |
| Vertical length of upper torso | L | 3 ft | Noneon both sides of equation |
| Mass of diffuse cloud of brain matter | mcloud | 0.3 lb | 0.10.8 lb |
| Exit speed of cloud of brain matter | vcloud | 300 ft s-1 | 0600 ft s-1 |
| Potential energy created by bullet's breaking and transiting skull | PE | 300 ft-lb | 0600 ft-lb |
| Lever arm of rotation of head about top of neck | Rhead | 4.5 in | 3.55.5 in |
| Lever arm of bullet with respect to top of neck | Rbullet | 5.75 in | 4.756.75 in |
| Mass of large fragment 1 | mfrag1 | 0.027 lb | 0.0220.032 lb |
| Exit velocity of large fragment 1 | vfrag1 | 500 ft s-1 | 250750 ft s-1 |
| Upward angle of large fragment 1 | Θfrag1 | 40° | 20°60° |
| Mass of large fragments 2,3 | mfrags23 | 0.01 lb | 0.0050.015 lb |
| Exit velocity of large fragments 2,3 | vfrags23 | 500 ft s-1 | 250750 ft s-1 |
| Upward angle of large fragments 2,3 | Θfrags23 | 70° | 50°90° |
| Final speed of forward snap of head | vsnap | Calculated | Calculated |
| Final speed of rearward mechanical recoil (lurch) of head and upper torso | vbodyafter, vlurch | Calculated | Calculated |
| Half-angle of conical cloud of brain matter | Θcl | 70° | 20°120° |
| 3-D term for speed of cloud (to reduce mean X-velocity) | fxcl | Calculated | Calculated |
| 3-D terms for kinetic energy of large fragment 1 (to add Y, Z components of KE) | fkefrag1 | 1.25 | 1.01.5 |
| 3-D term for kinetic energy of large fragments 2,3 (to add Y, Z components of KE) | fkefrags23 | 1.25 | 1.01.5 |
| 3-D term for kinetic energy of lurching body (to add Y, Z components of KE) | fkebody | 1.2 | 1.01.4 |
| Distance of bullet's transit through head | dtransit | 4 in | 08 in |
| Distance of forward snap of head | dsnap | 2.2 in | 1.62.8 in |
| Distance moved by large fragments in Z313 | dfrags | 6 ft | 210 ft |
| Time delay to begin snap after Z312 closes | tdelay | 0.002 s | 0.0000.007 s |
| Time duration of forward snap within 312,313 | tsnap | Calculated | Calculated |
| Time for bullet to transit the head | ttransit | Calculated | Calculated |
| Time of lurch within open period of Z313 | tlurch | Calculated | Calculated |
| Factor for improved moment of inertia of body | fI | 1.11 | 1.061.16 |
Mass of bullet, mbullet
The mass of the WCC/MC bullet is one of the best-known values
used here. Weights of unfired WCC/MC bullets generally fell between 160 and 161
grains, according to FBI Agent Robert A. Frazier (WCR 95). Larry Sturdivan used
a figure of 162 grains in his testimony to the HSCA. Dr. John K. Lattimer
reported in his book Kennedy and Lincoln (p. 287) that 100 WCC/MC bullets
from lots 6000, 6001, 6002, and 6003 averaged 160.8 grains. Thus I used 161
grains for the default weight and a range of 5 either way just to be sure.
Entrance velocity of bullet, vbullet
The Warren Commission determined that the bullet would have
impacted the president's head with a speed of just over 1800 ft s-1. I used
1800, with a range of 50 ft s-1 either way.
Exit velocity of bullet, vbulletafter
It is difficult to know the exit speed of the bullet, or
strictly speaking, the two large pieces of the bullet. There were evidently
going fast enough to dent the windshield and the chrome strip above it, which
would have required some hundreds of feet per second. I finally settled on a
default value of 200 ft s-1, with a range of 200 ft s-1
either way.
Angle of bullet above horizontal, Θ
It is impossible to know this angle precisely. According to
the Warren Commission (WCR 110), the angle of declination for the third shot was
just over 15°. The downward inclination of the street of 3° makes the
effective angle 12° relative to the car. I used a range of ± 5°,
which includes all reasonable angles.
Mass of head, mhead
Believe it or not, the mass of the head is among the hardest
variables to get a good value for. The best estimate I can presently make is around 78
lb. Here are the steps I
went through to estimate the mass.
(1) I looked in Gray's Anatomy, but found that it
wasn't very usefulit is mostly descriptive and qualitative. One interesting
fact, though (p. 390), was that the cranial capacity of the average male
European is >1450 cm3. (Gray's Anatomy: Descriptive and Applied,
34th Edition, 1967, Longmans, Green and Co., Ltd., London, 1669 pp. Editor: D.V.
Davies.)
(2) I found a great book with lots of quantitative
information: The Human Skeleton in Forensic Medicine, by Wilton Marion
Krogman, Ph.D., LL.D. (h.c.), Charles C. Thomas, Publisher, Springfield, IL,
1962, 337 pp.
(3) Krogman refers to a study by N.W. Ingalls (Ingalls N.W.,
1915, "Observations on bone weights," Amer. J. Anat. 48(1), 4598),
who studied the skeletons of 100 adult white Americans and found that the head
(cranium + mandible + teeth) weighed 14.9% of the total skeleton + teeth).
(4) Another study cited by Krogman (Lowrance E.W. and Latimer
H.B., 1957, Weights and linear measurements of 105 human skeletons from Asia. Amer.
J. Anat. 101, 445459) showed
that for the Asian skeletons, the skull + mandible accounted for 20.2% of the
dry weight of the skeleton.
(5) Krogman also cites (on p. 232) a study by Baker and
Newman (Baker P.T. and Newman R.W., 1957, "The use of bone weight for human
identification," Amer. J. Phys. Anthropol. n.s. 15(4), 601618)
that related skeletal weight to living weight. The regression equation for white
males killed in the Korean war was:
Living weight (lb) = 0.024(Dry skeletal wt., g) + 50.593 lb (± 20.1 lb)
The authors noted that the regression was weak,
i.e., that there was only an indirect relation between skeletal and living
weights. (This presumably meant that heavy-set men had skeletons more similar to
their slimmer colleagues.)
Converting all the units to pounds gives the following
equation:
Living weight (lb) = 10.90(Dry skeletal wt., lb) + 50.6
This is equivalent to:
Dry skeletal wt. (lb) = [Living wt. (lb) - 50.6 (± 20.1)]/10.90
= 0.0918(Living wt., lb) - 4.64 (± 1.84)
This relation allows us in
principle to take a person's living weight and get their skeletal weight, which
then can be multiplied by 15% to get the dry weight of their head.
We can test this approach on JFK. If he weighed 175 lb, his
dry skeleton would weigh:
0.0918(175) - 4.64 (± 1.84) = 16.06 - 4.64 = 11.42 lb (± 1.84)
15% of this for the skull plus teeth would be
1.71 lb (± 0.28). Adding >1450 g for the cranial tissue brings the total to
1.71 lb + (>3.19 lb) = >4.9 lb. To this we need to add the additional
weight of wet cranial bones and noncranial tissue. Assuming (without much
justification) a wet/dry ratio of 2 for bones, the weight becomes 3.42 +
(>3.19) lb (± 0.56), or >(6.057.17) lb. A reasonable value might be 8
lb or so.
(6) In a direct measurement, A.E. Snyder and his wife M.M.
Snyder attempted to weigh the former's head by resting it on a bathroom scale,
and got 8 lb.
(7) I estimated the weight of of my head by measuring its
dimensions and multiplying by a density of 1 g m-3, the density of
water. Assuming my head to be box-shaped, I found maximum dimensions of 9 in
high, 4.5 in wide, and 5.5 in deep, or 223 in3. That gave a weight of
<5.9 lb. But my head is small, even for my height of 5 feet 10 inches; JFK's
would surely have been larger and heavier. A weight of 78 lb would be
reasonable.
(8) Lastly, my head-snap calculations shown below best
matched the Z-film for weights of the head less than 10 lb.
(9) This gives four estimates of the weight of the head:
>(6.057.17) lb from my skeletal calculations, 8 lb from Snyder's direct
measurement on himself, 78 lb or so from the volume of my head extrapolated
to JFK's, and <10 lb from my head-snap calculations. In the end, I took 7
lb as the best starting point, and calculated for a range of 410 lb.
Mass of upper torso, mbody
The mass of JFK's upper torso cannot be known to within 10 or
20 lb because it was not measured. I just took his total weight at autopsy
(about 170 lb) and divided it by two, to get 85 lb. As a range, I used ±
20 lb.
Vertical length of upper torso, L
This variable is used to calculate the individual angular
momentum terms in the conservation equation for the lurch. It cancels out from
both sides of the equation, however, and so does not have to be known
accurately. I used 3 ft, which represents half his height at autopsy (72-½ in).
Mass of diffuse cloud of brain matter, mcloud
The mass of the diffuse cloud is very hard to determine, and cannot be known accurately. But we can take a reasonable guess,
starting from Lattimer's observation that 70% of the right cerebral hemisphere was
missing, and the reported weight of the remaining brain of 1500 g. That means
that the 1500 g represents something more than 65% of the original brain. If we
exaggerate and say that the brain is half cerebrum and half cerebellum, the 35% blown out
would correspond to roughly 17% of the full brain, or 307 g (0.7 lb). Thus
we could probably put the mass blown out at 01.5 lb or so.
The subject is made trickier by the fact that the mass of the
diffuse cloud, which is the whitish cloud seen close to JFK's head in frame 313
and to a lesser extent in frame 314, is not the same thing as the total mass
blown out in the forward direction. Large particles covered the entire front of
the car ahead of JFK. Whether they came from the explosion or simply accompanied
the initial rupture of the head above the right ear is debatable. If the latter,
then they represent forward momentum associated with the penetration phase of
the head shot. If the former, they represent the balance of momentum and energy
in the second, or explosive, phase. My initial reaction was to consider all the
missing mass as part of the diffuse cloud from the explosion, and that is what
this document does. The results for the mass have consistently come out in the
low end of this range (0.21.0 lb, and
most commonly 0.20.6 lb), however. As
default value I have used 0.3 lb, with a range of 0.10.8 lb.
Exit speed of cloud of brain matter
This variable is difficult enough to estimate that I
have solved for it in many of the simulations. About the only limitation I can
think of is the speed of sound, for the explosion probably would not have had
enough energy to expel the particles at supersonic speeds. When I set a speed,
it was usually 300 ft s-1. Values in this range were later confirmed
by examining the constraints on the variables.
It is easy to be confused by the fact that the tiny particles
in the diffuse cloud are rapidly slowed by friction in the air. The only
velocity that counts, however, the the one they had immediately on exit.
It must also be recognized that different particles will have
different exit speeds, with the smallest generally moving the fastest. A later
refinement to the calculations will incorporate a distributions of velocities,
but it will probably not improve the results noticeably. For now, it is enough
to consider the single speed of the diffuse cloud as representing the average of
a distribution of speeds.
Potential energy created by bullet's breaking and transiting skull, PE
The potential energy term is one of the easier ones to
fix accurately. According to Dr. Steve Cogswell of the the Armed Forces
Institute of Pathology, whom I spoke with a few years ago, most of the kinetic
energy of the bullet remains as kinetic energy when it hits the head. It
possesses nearly 1200 ft-lb of KE as it approaches the head. This figure is then
reduced by five quantities of energy: two to break through the scalp (at
entrance and at exit), two to penetrate the cranium, and one to create a path
through the brain tissue. Dr. Cogswell gave me the following figures: about 200
ft-lb to stretch skin to the breaking point, 1020
ft-lb to cut skin with a knife, and 3070 ft-lb to create a linear fracture in
the cranial vault. He also noted that the second cut (exiting) was easier
because of the first cut in the rear. He said that in the aggregate, it would
take 200300 ft-lb to break the skull and the skin. He considered 200 ft-lb to
be reasonable and 300 to be "conservative." For this reason I have
used as default the conservative value of 300 ft-lb for the potential energy in these
calculations, with a range of 0600. The more-extensive
tests of the critical variables at the end (the sections on constraints of the
critical variables) gave a range of 100600 ft-lb for the KE, which is
completely consistent with the above data.
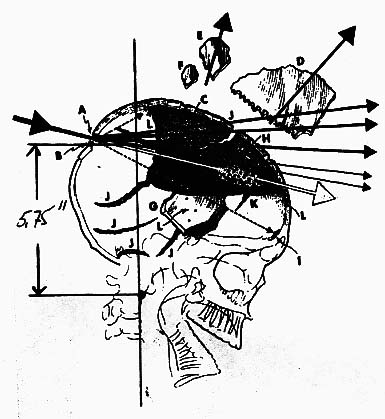
Lever arm of rotation of head about top of neck, Rhead
This variable is based on imagining the head to be a
sphere of diameter 9 in that rotates about the top of the neck after it is hit
by the bullet. Its effective "lever arm" of rotation is thus the
distance from the bottom of the head to its center of gravity (its geometric
center), or its radius (4.5 in). For the sensitivity tests, the lever arm is
given a range of ± 1 in, for a total range of 3.55.5
in.
Lever arm of bullet with respect to top of neck, Rbullet
This variable represents the vertical distance between
the path of the incoming bullet and the point of rotation of the head at the top
of the neck. The value of 5.75 in is based on the bullet's entering the head 2
in below the top and at a downward angle of 18° above the horizontal, as shown
in Figure 90 on page 216 of Dr. Lattimer's
book Kennedy and Lincoln. The diagram was scaled by a factor of 3.3
to get a head with diameter 9 in. Like Rhead, it is given a
range of ± 1 in for sensitivity tests.

Mass of large fragment 1, mfrag1
The mass of large fragment 1, the largest of the three
large fragments that were exploded from the head, can be estimated from its
dimensions and its density. The estimates need not be precise because the
fragments are small parts of the final solution. According to Dr. John
Lattimer (Kennedy and Lincoln, p. 156), the largest fragment was
"triangular, approximately 6.5 by 7.5 cm." That would give it an area
of 24.4 cm2. Assuming it to be 0.5 cm thick and of unit density, its
mass is 12.2 g, or 0.027 lb. This is the default value used in all calculations
here. For sensitivity tests it is given a range of ±
0.005 lb, or an overall range of 0.0220.032 lb.
Exit velocity of large fragment 1, vfrag1
In principle, the exit velocity of the large fragments
can be estimated from their distance traveled in frame 313 and the time that
represents. The distance is about 6 ft. The time, however, is not known exactly
because the fragments were ejected some time after frame 313 opened (because the
paths of the rotating fragments extend into the head). The time must lie between
0 ms and 25 ms, corresponding to the known exposure time of 1/40 sec for
Zapruder's camera (Zavada report, page 15 of Part 4). The slowest this speed
could be is 6 ft divided by the longest time (0.025 s), or 240 ft s-1.
To cover all possible situations, I have used a default value of 500 ft s-1
and a range of ± 250 ft s-1, for an
overall range of 250750 ft s-1. Again, however, the exact value
for this speed is unimportant because the large fragments contribute little to
the final solution.
Upward angle of large fragment 1, Θfrag1
This angle can be measured directly from any photo of
frame 313. It is about 40°. To be conservative, I used an overly large range,
20°, for an overall range of 20°60°.
Mass of large fragments 2,3, mfrags23
Large fragments 2 and 3 are grouped together here
because of Lattimer's figure (ibid., p. 90) that shows them both moving upward
at similar angles. (This assumption is not critical, however, because the
fragments do not contribute importantly to the final solution.) Fragment 2 is
roughly a square of side 2.5 cm; fragment 3 is the same but of side 1.5 cm. That
makes their areas 6.25 cm2 and 2.25 cm2, respectively.
Assuming that their thicknesses are also 0.5 cm and their densities 1 g cm-3,
as used for fragment 1, their masses will be 3.125 g (0.007 lb) and 1.125 g (0.002
lb). That makes a total mass of 4.25 g, or 0.009 lb, which we round to 0.01 lb
for the default value. This is given a range of ± 0.005
lb, for an overall range of 0.0050.015 lb.
Exit velocity of large fragments 2,3, vfrags23
Since large fragment 2 seemed to move about the same
distance as large fragment 1 (6 ft), I have used the same default value of 500
ft s-1 and range of ± 250 ft s-1
as for fragment 1.
Upward angle of large fragments 2,3, Θfrags23
This angle can also be measured
directly from any photo of frame 313. It is about 70°. I used the same large
range, 20°, as for fragment 1, for an overall range of 50°90°.
Final speed of forward snap of head, vsnap
The value of this variable is calculated from the amount
of momentum or angular momentum transferred to the head from the bullet. It is
important to understand that these calculations give the final speed of the
snap, not the average speed as determined from frames 312 and 313 of the
Zapruder film. Although the final speed will be larger than the average speed,
it may not differ significantly from it. The difference is neglected here
because we are primarily interested in determining whether the calculations can
reproduce the general nature of the snap. We recognize that we cannot go farther
than this because we cannot determine the exact speed of the snap.
Final speed of rearward mechanical recoil ( lurch) of head and upper torso,
vbodyafter, vlurch
This is the big unknown that we are trying to reproduce.
As with the forward snap, we must recognize that we cannot know the final speed
of the rearward mechanical recoil (the value calculated here), only the speed averaged over one frame. Thus
we can only determine whether the mechanical simulations reproduce the general
nature of the immediate recoil (something like 0.51.0
ft s-1 rearward).
Half-angle of conical cloud of brain matter, Θcl
I have found it convenient to envision
the cloud of exploded brain matter as a cone centered on the X-axis. The
variable Θcl
represents the half-angle of that cone, or the angle between the axis and the
outermost lateral extent of the cloud. I originally set the default value to a
conservative (broad) 45°, which covered the entire forward part of the car and then some.
I thought it was
probably too large. But then I realized that a number of lines of evidence
pointed to its being larger still, such as the large fragment that exited at
70°, the broad diffuse cloud seen in frame 313, and the results of the later
simulations that seemed to require a wider could in order to reduce the speed of
the lurch to the observed value. I then increased the default value to
70°, and broadened the range from its earlier ±
20° to ± 50°, for a total range of
20°120°.
3-D term for speed of cloud (to reduce mean X-velocity), fxcl
This term is a factor that takes account of the lateral
movement of part of the cloud of fragments to find the net X-component of the
cloud's velocity. It is calculated from the half-angle of the cloud, Θcl,
by averaging the X-component of the conical cloud over the Y- and Z-axes (really
a simple double integral). The resulting formula for the average is given with
each of the simulations in which it is used. The value of fxcl
ranges between 1 (for a pencil-like cone) and 0 (for a spherical
"cone." There is no strict default value for fxcl
because it is always calculated from Θcl.
But at the default half-angle of 70°, fxcl = 0.59, and at
90° it is 0.40.
3-D term for kinetic energy of large fragment 1 (to add Y component of
KE), fkefrag1
This variable express the fact that
3-D velocities of large fragment 1 will add kinetic energies corresponding to
the component of the of the velocity along the Y axis. (X- and Z-components are
already included in vfrag1.) If we imagine that the maximum Y
component of KE could equal typical X or Z components, the maximum fkefrag1
would be (2 + 1)/2, or 1.5. The actual value is probably less than this,
however, because there is no evidence that large fragment 1 moved so much
sideways. For this reason, I set the default value at 1.25, which is midway
between the minimum 1.0 and the maximum 1.5. I then gave a range of ±
0.25 in order to encompass the full range of 1.01.5.
3-D term for kinetic energy of large fragments 2,3 (to add Y component of
KE), fkefrags23
Same as for fkefrag1.
3-D term for kinetic energy of lurching body (to add Y component of KE),
fkebody
This term functions similarly to the 3-D term for the
large fragment in that it adds KE to that seen in the X-motion. In this case, only
Y-motion (into and out of the plane of the film) needs to be added, because the
body cannot move vertically. This term will also be quite small, because
although JFK moved "back and to the left," he clearly moved more back
than to the left. Had he moved as much to the left as to the back, fkebody
would be 2 (an additional equal amount of KE to the left). Somewhat arbitrarily,
I estimate that an additional 20% KE would be added from the leftward motion,
which gives a default value of 1.2. To express the large uncertainty in this
value, I give it a range of ± 0.2, for an overall
range of 1.01.4. Perhaps the most important thing to remember about this
term, however, is that it has virtually no effect on the answer, because the KE
of the body also have virtually no effect.
Distance of bullet's transit through head, dtransit
This number can be read directly from Figure 90 on page 216 of Dr. Lattimer's
book Kennedy and Lincoln. I got 4 inches. To be conservative, I gave it
the large range of 08 inches.
Distance of forward snap of head, dsnap
This variable may seem obvious, but it is not. From
Josiah Thompson's measurements reported in Six Seconds in Dallas, it
appears to be 2.2 inches. But the actual value could be greater or less than
this, depending on whether the snap continued past the closing of the
shutter in frame 313 or quit before it closed. Thus we are fundamentally limited
in what we can say about it. In response to this lack of precision, I have used
a range of ± 0.6 in, for a total range of 1.62.8 in.
Distance moved by large fragments in Z313, dfrags
This number can be read directly from any display of
frame 313. It is about 6 ft. To be conservative, I used a range of ±
4 ft, to give a total range of 210 ft.
Time delay to begin snap after Z312 closes, tdelay
This is the time from the end of the exposure of frame 312
until the bullet hits the head. It is given a nominal value of 2 ms and a range
of 07 ms. It expresses the notion that the
bullet might not have hit the minute that frame 312 was over, and in fact
probably didn't.
Time duration of forward snap within 312,313, tsnap
This variable represents the total time taken for the head to
snap forward. It is estimated from the distance moved (provided) and the speed
of the snap (calculated from other independent variables).
Time for bullet to transit the head, ttransit
The time of transit is calculated from the average speed of
the bullet through the head and the distance of transit.
Time of lurch within open period of Z313, tlurch
This variable refers to the time within the exposed period of
frame 313 that the head and body have already been lurching rearward. It is
estimated by subtracting the sum of the other three times (tdelay,
tsnap, ttransit) from the total time of a
frame (55 ms).
Factor for improved moment of inertia of body, fI
The angular calculations require the moment of inertia
of JFK's upper body about the point of rotation (the base of his spine). I
originally considered his upper body to be a rod and used the appropriate
formula. Later I decided to try to improve the estimate. I broke the upper body
spherical head and cylindrical neck, torso, and outstretched arms, assigned
weights to each based on their relative volumes, and recalculated carefully. I
got a now moment of inertia that was 11% greater than the original. To preserve
all the earlier calculations and to allow myself to vary this shape factor, I
created I and gave it the default value of 1.11. For sensitivity tests, I
allowed it to vary by ± 0.05, for a total range of
1.061.16.
Ahead to Snap Linear
Back to Wound Ballistics
Back to Physics of the Head Shot