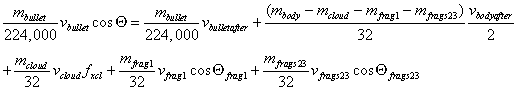
11. Lurch 3 Linear—add 3-D motion of the diffuse cloud
The model and its justification
Like Lurch 2 Linear, Lurch 3 Linear calculates the speed of
the rearward lurch of the upper body from the bullet, the body, the cloud, and the
large fragments. To these it adds
three-dimensional motion of the diffuse cloud. This three-dimensionality
decreases the intensity of the lurch dramatically, from -2.44 ft s-1
to -0.88 ft s-1 for default
values of the variables. This result shows that the 3-D motion of the diffuse
cloud is an extremely important property to consider.
Solving the simultaneous equations
As before, the equations for conservation of X-momentum
and total energy are solved simultaneously. To the version in Lurch 2 are added
two terms that express the three-dimensionality of the motion of the diffuse
cloud—fxcl and fkecl.
The fxcl expresses something like the fraction of a
horizontal two-dimensional velocity that is in the forward direction.
Specifically, fxcl is the average of cos Q
between the leftmost forward angle considered reasonable and the rightmost. If
all the cloud is considered to move straight ahead, fxcl = 1.
If the cloud is 30° wide, fxcl = 0.94. If the cloud extends
from -90° to +90°, which means from straight right to straight left, fxcl
is 0.4. For the starting value, I used the intermediate 0.7. For the range, I
used 0.4–1. Of course, the real cloud was three-dimensional rather than
two-dimensional. The third dimension is added in Lurch 3 Angular.
The fkecl term expresses the kinetic energy
of the cloud beyond what is contained in the X-component of the velocity of the
exiting fragments (i.e., for pure forward motion). If the cloud is shot out
equally in all three directions (like an expanding sphere), then KEx
= KEy = KEz and fkecl = 3.
If it is shot out as an octant, a quadrant, or a hemisphere, the same relations
hold. This will make the maximum value of fkecl equal to 3 and
the minimum equal to 1. For this reason, I used a starting value of 2 and a
range of 1–3.
The solutions for vbodyafter and vcloud,
-0.88 ft s-1 and 309 ft s-1, respectively, are shown below
the variables. Both are drastically reduced from Lurch 2 Linear.
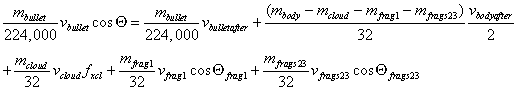
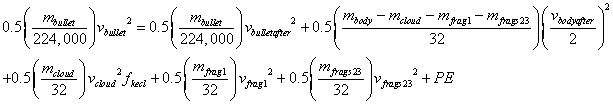
Default values of the variables
| mbullet = 161 gr | vbullet = 1800 ft s-1 | mfrag1 = 0.027 gr |
| mbody = 85 lb | vbulletafter = 200 ft s-1 | mfrags23 = 0.01 gr |
| mcloud = 0.3 lb | Qfrag1 = 40° | vfrag1 = 300 ft s-1 |
| Q = 17° | Qfrags23 = 70° | vfrags23 = 300 ft s-1 |
| PE = 200 ft-lb | fxcl = 0.7 | fkecl = 2 |
vbodyafter = -0.88 ft s-1 vcloud = 309 ft s-1
| Momentum | Energy, ft-lb | ||
| Before | After | Before | After |
| Pbullet = 1.24 | Pbulletafter = 0.14 | KEbullet = 1164 | KEbulletafter = 14 |
| Pbodyafter = -1.16 | KEbodyafter = 0.3 | ||
| Pcloud = 2.03 | KEcloud = 898 | ||
| Pfrag1 = 0.19 | KEfrag1 = 38 | ||
| Pfrags23 = 0.03 | KEfrags23 = 14 | ||
| PE = 200 | |||
Sensitivity analysis
Sensitivity analysis, Lurch 3 Linear
(Standard
conditions in boldface)
|
mbullet |
vlurch |
mbody |
vlurch |
mcloud |
vlurch |
PE |
vlurch |
vbullet |
vlurch |
|
156 |
-0.874 |
|
|
|
|
|
|
1750 |
-0.85 |
|
157 |
-0.875 |
65 |
-1.151 |
|
|
0 |
-1.042 |
1760 |
-0.856 |
|
158 |
-0.876 |
70 |
-1.069 |
|
|
50 |
-1.003 |
1770 |
-0.862 |
|
159 |
-0.877 |
75 |
-0.997 |
0.1 |
-0.23 |
100 |
-0.963 |
1780 |
-0.868 |
|
160 |
-0.878 |
80 |
-0.935 |
0.2 |
-0.597 |
150 |
-0921 |
1790 |
-0.873 |
|
161 |
-0.879 |
85 |
-0.879 |
0.3 |
-0.879 |
200 |
-0.879 |
1800 |
-0.879 |
|
162 |
-0.88 |
90 |
-0.83 |
0.4 |
-1.118 |
250 |
-0.836 |
1810 |
-0.885 |
|
163 |
-0.881 |
95 |
-0.786 |
0.5 |
-1.329 |
300 |
-0.791 |
1820 |
-0.891 |
|
164 |
-0.882 |
100 |
-0.747 |
0.6 |
-1.52 |
350 |
-0.745 |
1830 |
-0.897 |
|
165 |
-0.883 |
105 |
-0.711 |
0.7 |
-1.696 |
400 |
-0.698 |
1840 |
-0.903 |
|
166 |
-0.884 |
|
|
0.8 |
-1.861 |
|
|
1850 |
-0.908 |
|
Sensitivity = |
Sensitivity = |
Sensitivity = |
Sensitivity = |
Sensitivity = |
|||||
|
Range = 0.01 |
Range = 0.44 |
Range = 1.63 |
Range = 0.34 |
Range = 0.06 |
|||||
|
vbulletafter |
vlurch |
Q |
vlurch |
mfrag1 |
vlurch |
mfrags23 |
vlurch |
vfrag1 |
vlurch |
|
|
|
12 |
-0.858 |
0.022 |
-0.858 |
0.005 |
-0.873 |
|
|
|
0 |
-0.783 |
13 |
-0.862 |
0.023 |
-0.862 |
0.006 |
-0.874 |
100 |
-0.81 |
|
50 |
-0.809 |
14 |
-0.866 |
0.024 |
-0.867 |
0.007 |
-0.876 |
150 |
-0.83 |
|
100 |
-0.834 |
15 |
-0.87 |
0.025 |
-0.871 |
0.008 |
-0.877 |
200 |
-0.848 |
|
150 |
-0.858 |
16 |
-0.874 |
0.026 |
-0.875 |
0.009 |
-0.878 |
250 |
-0.865 |
|
200 |
-0.879 |
17 |
-0.879 |
0.027 |
-0.879 |
0.010 |
-0.879 |
300 |
-0.879 |
|
250 |
-0.9 |
18 |
-0.884 |
0.028 |
-0.884 |
0.011 |
-0.881 |
350 |
-0.892 |
|
300 |
-0.918 |
19 |
-0.89 |
0.029 |
-0.888 |
0.012 |
-0.882 |
400 |
-0.903 |
|
350 |
-0.935 |
20 |
-0.896 |
0.030 |
-0.892 |
0.013 |
-0.883 |
450 |
-0.911 |
|
400 |
-0.951 |
21 |
-0.902 |
0.031 |
-0.896 |
0.015 |
-0.884 |
500 |
-0.918 |
|
|
|
22 |
-0.908 |
0.032 |
-0.9 |
0.015 |
-0.885 |
|
|
|
Sensitivity = |
Sensitivity = |
Sensitivity = |
Sensitivity = |
Sensitivity = |
|||||
|
Range = 0.17 |
Range = 0.05 |
Range = 0.04 |
Range = 0.01 |
Range = 0.11 |
|||||
|
vfrags23 |
vlurch |
Qfrag1 |
vlurch |
Qfrags23 |
vlurch |
fxcl |
vlurch |
fkecl |
vlurch |
|
100 |
-0.874 |
20 |
-0.913 |
50 |
-0.901 |
|
|
1 |
-1.515 |
|
150 |
-0.876 |
25 |
-0.906 |
55 |
-0.896 |
0.4 |
-0.222 |
1.25 |
-1.286 |
|
200 |
-0.878 |
30 |
-0.898 |
60 |
-0.891 |
0.5 |
-0.441 |
1.5 |
-1.117 |
|
250 |
-0.879 |
35 |
-0.889 |
65 |
-0.885 |
0.6 |
-0.66 |
1.75 |
-0.985 |
|
300 |
-0.879 |
40 |
-0.879 |
70 |
-0.879 |
0.7 |
-0.879 |
2 |
-0.879 |
|
350 |
-0.879 |
45 |
-0.868 |
75 |
-0.873 |
0.8 |
-1.098 |
2.25 |
-0.792 |
|
400 |
-0.878 |
50 |
-0.856 |
80 |
-0.867 |
0.9 |
-1.318 |
2.5 |
-0.717 |
|
450 |
-0.876 |
55 |
-0.843 |
85 |
-0.861 |
1.0 |
-1.537 |
2.75 |
-0.653 |
|
500 |
-0.874 |
60 |
-0.828 |
90 |
-0.855 |
|
|
3 |
-0.598 |
|
Sensitivity = |
Sensitivity = |
Sensitivity
= |
Sensitivity = |
Sensitivity = |
|||||
|
Range = 0.00 |
Range = 0.08 |
Range = 0.05 |
Range = 1.32 |
Range = 0.92 |
|||||
Ordered summary of sensitivities
| Variable | Sensitivity of vlurch | Range of vlurch, ft s-1 | Magnitude |
| Positive effect on lurch (reduces rearward velocity) | |||
| vfrags23 | 0.000 | 0.00 | Small |
| Qfrags23 | 0.096 | 0.05 | Small |
| Qfrag1 | 0.096 | 0.08 | Small |
| PE | 0.19 | 0.34 | Small |
| mbody | 1.02 | 0.44 | Small |
| fkecl | 0.88 | 0.92 | Medium |
| Negative effect on lurch (increases rearward velocity) | |||
| mfrags23 | -0.017 | 0.01 | Small |
| mbullet | -0.18 | 0.01 | Small |
| mfrag1 | -0.138 | 0.04 | Small |
| Q | -0.097 | 0.05 | Small |
| vbullet | -1.23 | 0.06 | Small |
| vfrag1 | -0.092 | 0.11 | Small |
| vbulletafter | -0.096 | 0.17 | Small |
| fxcl | -1.74 | 1.32 | Large |
| mcloud | -0.89 | 1.63 | Large |
Making the cloud three-dimensional not only changed the basic solution (see above), but also the hierarchy of sensitivities. Into second and third place for effect (range of lurch) moved the two spatial variables fxcl and fkecl. Only the effect of mcloud remained larger. All the other 12 variables had small effects on the solution. Thus the three important variables all had to do with the cloud—its mass and the three-dimensional distributions of its momentum and kinetic energy. In short, the properties of the diffuse cloud became all-important to calculating the lurch.
Summary
Adding three-dimensionality to the diffuse cloud
decreased the magnitude of the lurch by a factor of three, from -2.44 ft s-1
to -0.88 ft s-1. It also made the mass and dimensionality of the
cloud the most important variables (greatest range of lurch predicted from the
range of each of the variables). As much as anything, this result expressed the
difficulty is estimating the true attributes of the cloud.
Ahead to Lurch 4 Linear
Back to Lurch 2 Linear
Back to Physics